Лекция 16. Второй способ. Найдем передаточную функцию одномерного ОУ, управляемого от ЦВМ (рис

Второй способ. Найдем передаточную функцию одномерного ОУ, управляемого от ЦВМ (рис. 10),

т.е. найдем

, (29)

полагая известной передаточную функцию объекта управления

.

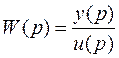Прежде всего, заметим, что передаточная функция любого линейного дискретного фильтра не зависит от вида входного сигнала, поэтому с целью определения передаточной функции 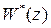ради простоты последующих операций примем в качестве управляющей последовательности единичную последовательность, т.е. будем считать, что

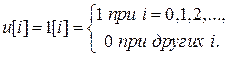
При этом на выходе фиксатора Ф (рис.10) образуется единичная

ступенчатая функция, т. е.

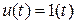
(рис. 11), что вытекает из модели фиксатора 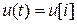, 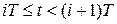(30).

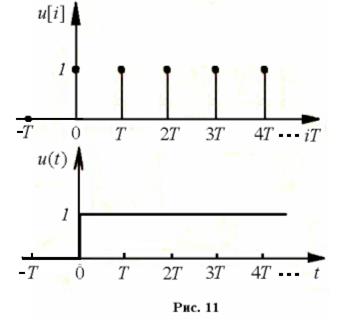
Реакция объекта управления на единичную ступенчатую функцию есть его переходная характеристика h(t). Следовательно, в этом случае управляемая последовательность

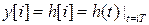
представляет собой переходную последовательность h[i] объекта управления. Учитывая, что Z-преобразование управляющей последовательности

,

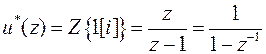и принимая во внимание, что

,

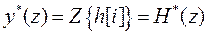где 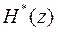- Z-преобразование переходной последовательности объекта управления, из 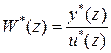(29) находим искомую передаточную функцию

.

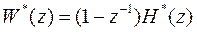Переходную характеристику объекта управления можно определить как обратное преобразование Лапласа:

.

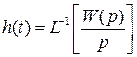Поэтому функцию 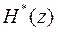записывают в символическом виде

.

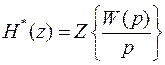Отсюда получаем следующее выражение для передаточной функции объекта, управляемого от ЦВМ,

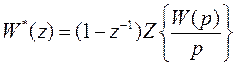. (31)

В соответствии с этой формулой для определения 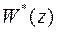по известной передаточной функции 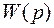надо:

1) определить оригинал преобразования Лапласа 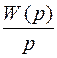, т.е. найти h(t);

2) найти Z-преобразование ;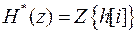

3) произвести умножение на .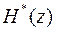

Обычно для выполнения первых двух этапов используют таблицу Z-преобразований.

Пример. Найдем передаточную функцию двойного интегратора, управляемого от ЦВМ.

Пусть передаточная функция объекта управления (двойного интегратора) имеет вид .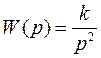

Из таблицы Z-преобразований и (31) имеем

,

,

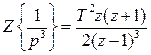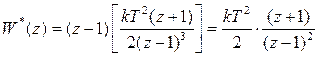что совпадает при k =1 с выражением, полученным в предыдущем примере другим путем.