Свойства Z-преобразования.

1. Теорема линейности.

Z-преобразование линейной комбинации двух последовательностей равно линейной комбинации Z-преобразований этих последовательностей

.

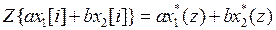Здесь 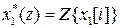, , 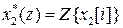a, b-постоянные.

2. Теорема смещения (сдвига).

Рассмотрим два случая, полагая, что k положительное целое число:

a. Смещение в сторону запаздывания на k-периодов дискретизации.

При этом Z-преобразование определяется следующим образом,

.

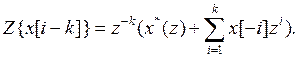b. Смещение последовательности в сторону опережения на k-периодов дискретизации.

При этом Z-преобразование определяется следующим образом,

(*)

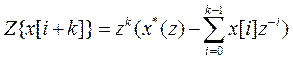Доказательство.

Введем новую переменную суммирования 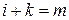,так что 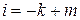. Тогда можно преобразовать к следующему виду

,

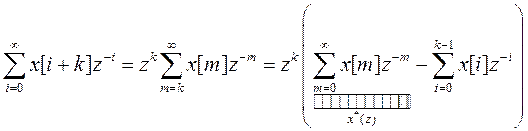что и требовалось доказать.

· Если 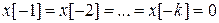, тогда .

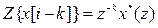· Если 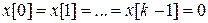, тогда .

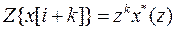3. Теорема о сумме свертки

Произведение Z-преобразовани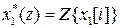й и 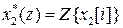равно Z-преобразованию от свертки их оригиналов

= .

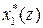
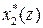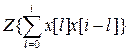4. Теорема о конечном значении.

Предел 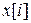при 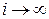опредлеляется следующим образом

,

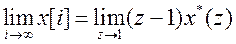если 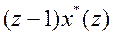не имеет полюсов на или вне окружности единичного радиуса комплексной плоскости Z.