Операторная форма записи линейных разностных уравнений.
В теории линейных дифференциальных уравнений удобно использовать понятие оператора дифференцирования. Для записи в операторной (символической) форме линейных разностных уравнений применяют оператор прямого сдвига Е на один период дискретизации в сторону опережения. Воздействие такого оператора на последовательность y[i]дает y[i+1], т.е.
Ey[i] = y[i+1].
Если еще раз приложить оператор Е к последовательности y[i], то получим последовательность
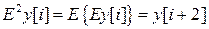 ,
,
смещенную в сторону опережения на два периода дискретизации. Продолжая этот процесс, приходим к выводу о том, что если k раз приложить оператор Е к последовательности y[i], то получим последовательность
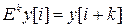 ,
,
смещенную в сторону опережения на k периодов дискретизации. Тогда, заменяя в (1)
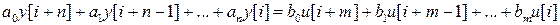 (1)
(1)
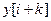 ,
, 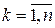 , на
, на 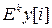 и
и 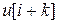 ,
, 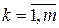 , на
, на  , вынося затем u[i] и y[i]за скобку справа, получаем символическую форму записи линейного разностного уравнения
, вынося затем u[i] и y[i]за скобку справа, получаем символическую форму записи линейного разностного уравнения
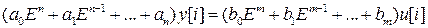 .
.
Вводя в рассмотрение выходной
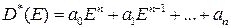
и входной
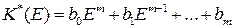
операторы Д-фильтра, получаем более компактную форму записи
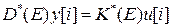 (5)
(5)
разностного уравнения (1).
Вводя с помощью выражений
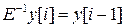 ,
, 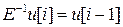
оператор обратного сдвига 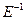 уравнение (2)
уравнение (2)
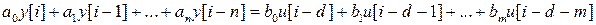 (2)
(2)
также можно записать в операторном виде
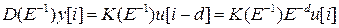 , (6)
, (6)
где операторные многочлены
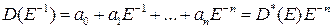
и
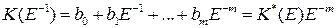
получаются из многочленов  и
и 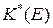 путем их умножения соответственно на
путем их умножения соответственно на 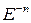 и
и 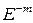 .
.
Если u[i]=0, i<0, то из (3) и (6) следует, что последовательность u[i] начинает оказывать влияние на выход Д-фильтра лишь спустя d периодов дискретизации после ее подачи на его вход. Таким образом, дискретный фильтр как бы включает в себя элемент запаздывания на dT секунд.
Дата добавления: 2015-08-14; просмотров: 1221;
