Прямое решение линейных разностных уравнений.

Линейное разностное уравнение описывает связь выхода и входа Д-фильтра лишь в неявной форме. Чтобы найти его реакцию на некоторую входную последовательность, надо это уравнение решить. Здесь, как и для непрерывных систем, знание поведения входной последовательности u[i] для

i = 0,1,2, ... и равенство ее нулю при i<0 позволяют получить лишь частичное описание выходной последовательности y[i] при i = 0,1,2. Для системы порядка n необходимо иметь n дополнительных данных, соответствующих начальным условиям в непрерывном случае. Однако в отличие от ситуации с дифференциальными уравнениями определение реакции Д-фильтра оказывается более простым делом. Покажем это, выразив уравнение (1) через последовательности, смещенные в сторону запаздывания. Заменяя в

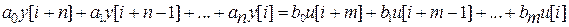(1)

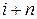( ) на i, т.е. полагая 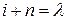, а затем, обозначая 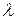как i , получаем другую форму записи разностного уравнения Д-фильтра

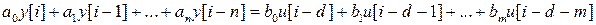, (2)

где 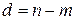. Здесь

, , , ,

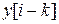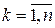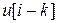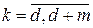представляют собой соответственно последовательности выхода и входа, смещенные в сторону запаздывания на k периодов дискретизации.

Полагая 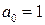, из (2) получаем рекуррентное соотношение

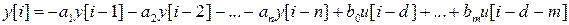, (3)

позволяющее определять выходную последовательность y[i], другими словами, реакцию Д-фильтра на входную последовательность u[i].

Отметим, что для уравнения (3) начальными условиями являются значения y[-1], y[-2],…,y[-n], которые будем считать заданными.

За начальный момент времени принимаем i=0.

Если хотя бы одно из значений y[-1] , y[-2] ,…, y[-n] не равно нулю, то говорят, что Д-фильтр предварительно возбужден.

Если y[-1]=y[-2]=…=y[-n]=0, то говорят, что Д-фильтр предварительно невозбужден.

Поставим задачу:

Пусть известна входная последовательность u[i]и начальные условия.y[-1] , y[-2] ,…, y[-n].

Требуется найти реакцию 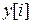Д-фильтра для i = 0, 1, 2, 3, ....

Эту задачу можно решитьс помощью прямого метода в силу того, что ЛРУ (3) является рекуррентным соотношением. Полагая i=0, из уравнения

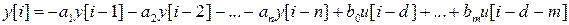(3)

получаем

,

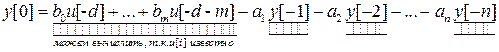Значение y[0] можно вычислить, т.к. u[i] задано, а начальные условия 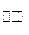известны.

Положим i=1 в (3), получаем

,

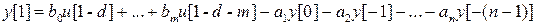( значение y[0] найдено на предыдущем шаге) и т. д. вычисляем y[2], y[3],…

Недостаток: ошибки округления.