Лекция 12. Пример. Рассмотрим дискретный интегратор (сумматор), описываемый разностным уравнением первого порядка

Пример. Рассмотрим дискретный интегратор (сумматор), описываемый разностным уравнением первого порядка

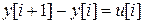. (5)

В данном случае 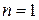, 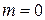. Пусть 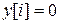, , 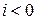а вход представляет собой единичную последовательность 1[i], т.е.

.

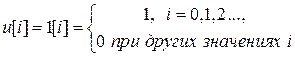Разрешая (5) относительно 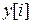, с помощью

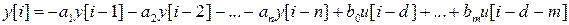(3)

получаем

.

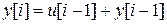Полагая i=0, 1, 2,… и используя на каждом шаге результаты вычислений, подученных на предыдущих шагах, с учетом равенства нулю u[i]и y[i]при i<0 находим последовательно

,

,

,

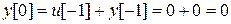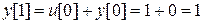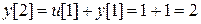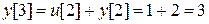
и т.д. Графики последовательностей u[i]и y[i]для этого примера показаны на рис. 5.

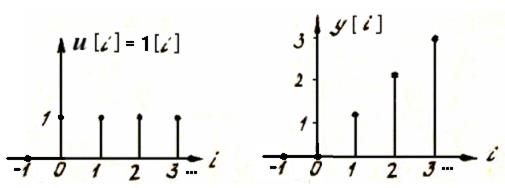
Рис. 5

Как видим, при нулевых начальных условиях, т.е. при ,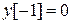

,

,

,

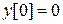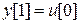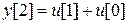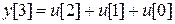
и т.д. Следовательно, при произвольной входной последовательности u[i]реакция равна

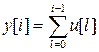, i=1,2…,

Заметим, что уравнение дискретного интегратора с учетом ненулевых начальных условий принято записывать в несколько ином виде:

,

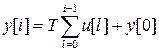где T- период дискретизации. Последняя формула соответствует алгоритму Эйлера численного интегрирования.

Заметим, что дискретный интегратор (сумматор) играет такую же существенную роль в теории цифровых систем, как интегратор – в теории непрерывных систем управления.