Операторная передаточная функция дискретного фильтра
Использование операторной формы записи разностных уравнений позволяет выразить зависимость "вход u[i]- выход y[i]" как рациональную функции от оператора прямого или обратного сдвига. Такую функцию, называемую операторной передаточной функцией или передаточным оператором, легко получить с помощью любого описания Д-фильтра (5) или (6).
Так, поделив формально левую и правую части уравнения 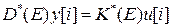 (5) на
(5) на  , получим
, получим
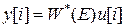 .
.
Следовательно, операторная передаточная функция 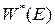 Д-фильтра имеет следующий вид:
Д-фильтра имеет следующий вид:
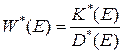 .
.
Ее можно выразить с помощью оператора обратного сдвига, если поделить уравнение 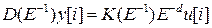 (6) на
(6) на 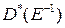 . При этом получаем
. При этом получаем
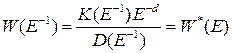 .
.
Заметим, что смысл деления уравнений (5) и (6) соответственно на  и
и 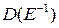 не ясен, так как это не обычные, а операторные многочлены. Можно показать, что обычные операции умножения и деления на многочлен от оператора сдвига допустимы, если начальные условия для разностного уравнения (2) равны нулю, т.е. если дискретный фильтр предварительно невозбужден.
не ясен, так как это не обычные, а операторные многочлены. Можно показать, что обычные операции умножения и деления на многочлен от оператора сдвига допустимы, если начальные условия для разностного уравнения (2) равны нулю, т.е. если дискретный фильтр предварительно невозбужден.
Пример. Рассмотрим дискретный интегратор. Из уравнения 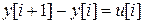 , описывающего дискретный интегратор, имеем
, описывающего дискретный интегратор, имеем
 .
.
Следовательно, получаем
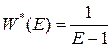 .
.
Так как в этом случае 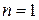 ,
, 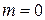 ,
, 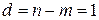 ,
, 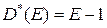 ,
, 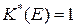 ,
,
то с учетом 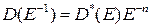 ,
, 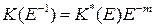
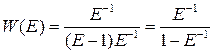 .
.
Дата добавления: 2015-08-14; просмотров: 1180;
