Уравнения дискретного фильтра в переменных состояния.
Современная теория цифровых систем управления, так же как и непрерывных, базируется на описании процессов в переменных состояния. До сих пор описывались модели Д- фильтров с одним входом и одним выходом, другими словами одномерных фильтров. Введем в рассмотрение многомерный дискретный фильтр, имеющий r входов и l выходов, который описывается векторными разностными уравнениями
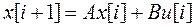 , (1)
, (1)
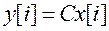 ,
,
где 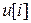 -
- 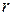 -векторная входная последовательность,
-векторная входная последовательность, 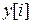 -
- 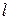 -векторная выходная последовательность, а
-векторная выходная последовательность, а 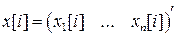 -
- 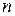 -векторная последовательность состояния, называемая вектором состояния. Компоненты вектора состояния
-векторная последовательность состояния, называемая вектором состояния. Компоненты вектора состояния 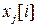 ,
, 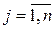 , называются переменными состояния дискретного фильтра. Матрицы А, В и С соответственно имеют размерности
, называются переменными состояния дискретного фильтра. Матрицы А, В и С соответственно имеют размерности 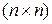 ,
, 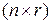 и
и 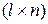 .
.
Первое из приведенных уравнений называется разностным уравнением состояния, а второе - разностным уравнением выхода. Для дискретного фильтра с одним входом и одним выходом, т.е. при 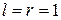 матрица В вырождается в вектор-столбец, а матрица С - в вектор-строку.
матрица В вырождается в вектор-столбец, а матрица С - в вектор-строку.
Так же как и для непрерывных систем, выбор переменных состояния для описания дискретных фильтров является неоднозначным, т.е. вид матриц А, В и С зависит от способа формирования переменных состояния. Заметим, что все приемы и методы преобразования матриц непрерывных систем пригодны для приведения матриц А и В к удобному виду, например, к диагональной форме или к канонической форме фазовой переменной (управляемой форме).
Пример. Преобразовать разностное уравнение

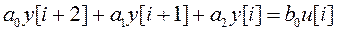
дискретного фильтра с одним входом и одним выходом в векторные разностные уравнения. В этом случае порядок фильтра n=2. Введя переменные состояния
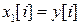 ,
,
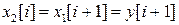 ,
,
так что  , получаем искомые уравнения
, получаем искомые уравнения
 ,
,
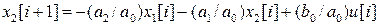 ,
,
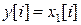 .
.
Следовательно, векторные разностные уравнения дискретного фильтра можно представить в виде (1), где
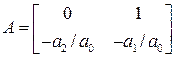 ,
, 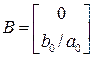 ,
, 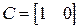 ,
, 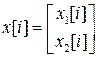 .
.
Дата добавления: 2015-08-14; просмотров: 1182;
