Дифференцирование вектора в подвижных координатах (Формула Бура)

Пусть вектор 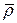представлен в подвижной системы координат в виде (рис.1.8):

.

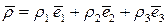Возьмём производную вектора 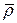по времени, учитывая, что орты подвижной системы координат изменяются по направлению:

.

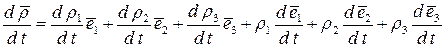Первые три слагаемые этой формулы дают нам относительную производную, обозначаемую как:

.

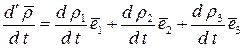Производная от единичного вектора — т. е. скорость конца этого вектора равна

.

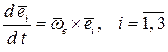Учитывая данное равенство, последние три слагаемых можно преобразовать следующим образом

.

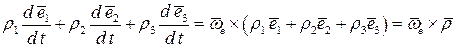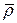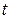Окончательно производная вектора по будет записываться соотношением:

,

где: 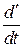— относительная (локальная) производная, в которой дифференцируются только координаты; 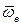— вектор угловой скорости подвижной системы координат.

Данная формула называется формулой Бура.