Теорема сложения скоростей
Абсолютная скорость точки при составном движении равна геометрической сумме переносной и относительной скоростей.
Пусть тело, с которой связана подвижная система координат, совершает произвольное движение относительно неподвижной системы координат. Это движение может быть рассмотрено как поступательное движение вместе с началом подвижной системой координат и сферическое относительно этого начала. Из векторного треугольника 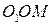 получаем
получаем
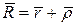 .
.
Вычислив проекции этого векторного равенства на оси неподвижной системы координат, получим уравнения движения точки М.
Относительное движение будет характеризоваться координатами точки в подвижной системе координат:
 .
.
Вычисляя производную вектора 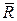 по времени с помощью формулы Бура, получим:
по времени с помощью формулы Бура, получим:
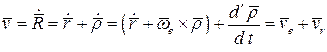 .
.
Сумма слагаемых, стоящих в скобке, даёт скорость точки твёрдого тела, с которым "сцеплена" подвижная система координат, совпадающей с исследуемой точкой в данный момент времени. Эту скорость называют переносной
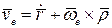 .
.
Относительная производная даёт относительную скорость
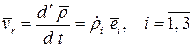 .
.
Дата добавления: 2015-08-08; просмотров: 692;
