Разложение движения плоской фигуры на поступательное и вращательное

Движение плоской фигуры можно разложить на поступательное, вместе с полюсом, и вращательное вокруг полюса. Полюсом называем произвольную точку, выбранную из каких-либо соображений для описания плоского движения.

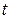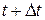Для доказательства рассмотрим два положения плоской фигуры в моменты времени и (рис.1.10). Переместим фигуру поступательно из положения 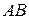в положение 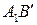. При этом точка 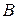описывает такую же траекторию как и точка 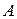. Затем повернём фигуру вокруг точки 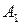на угол 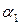так, чтобы точка 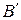заняла положение 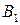. Перевод фигуры из начального положения в конечное можно произвести различными способами, выбирая за полюс вместо точки А любую другую, например, точку В. Заметим, что при этом поворот будет осуществляться на тот же угол и в том же направлении. Т. е. последнее из уравнений движения плоской фигуры является инвариантным (независимым) от выбора полюса. Значит и угловая скорость как производная от угла поворота не зависит от выбора полюса. Поступательное движение можно принять за переносное, а вращательное — за относительное.