Теорема о скоростях плоской фигуры

Скорость произвольной точки плоской фигуры равна геометрической сумме скорости полюса и скорости точки во вращательном движении вокруг полюса.

Подвижную систему координат выберем так, чтобы начало её совпадало с точкой А, принятой за полюс (рис.1.11). Рассмотрим движение произвольной точки В. Эта точка совершает составное движение, — поступательное вместе с подвижной системой координат и вращательное вокруг полюса. Согласно теореме сложения скоростей точки в составном движении, абсолютная скорость точки равна геометрической сумме переносной и относительной скоростей:

.

Рис. 1. 11. Скорости точек в плоском движении твердого тела

Но переносное движение является поступательным. Все точки, участвующие в нём, имеют одинаковые скорости, равные скорости полюса. Относительная скорость — это скорость во вращении точки В вокруг полюса.

.

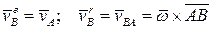Поэтому абсолютная скорость точки "В" может быть представлена в виде суммы

.

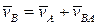Из доказанной теоремы вытекают два следствия:

· проекции скоростей точек плоской фигуры, расположенных на одной прямой, на направление этой прямой, равны друг другу;

· концы векторов скоростей точек прямолинейного отрезка на плоской фигуре располагаются на одной прямой и делят её на части, пропорциональные расстояниям между точками.

Эти следствия очевидны и иллюстрируются рис.1.12

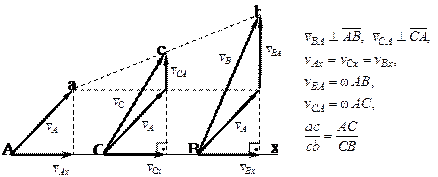
Рис. 1. 12. Теорема о сложении скоростей (следствия)