Мгновенный центр скоростей
В любой момент времени в плоскости фигуры при её непоступательном плоском движении существует одна единственная точка, скорость которой равна нулю. Эту точку называют мгновенным центром скоростей (МЦС).
Пусть скорость точки А плоской фигуры известна и равна 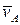 . Разложим движение на поступательное вместе с точкой А и вращение вокруг этой точки. Согласно теореме сложения скоростей (рис.1.13)
. Разложим движение на поступательное вместе с точкой А и вращение вокруг этой точки. Согласно теореме сложения скоростей (рис.1.13)
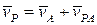 .
.
Будем искать положение такой точки, у которой скорость в данный момент времени равна нулю. Поэтому
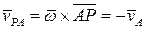 .
.
Из свойств векторного произведения следует, что вектор 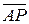 перпендикулярен векторам угловой скорости
перпендикулярен векторам угловой скорости 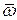 и скорости
и скорости 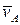 . Расстояние от точки А до искомой точки определится формулой
. Расстояние от точки А до искомой точки определится формулой
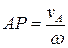
Найденная таким образом точка "Р" и является мгновенным центром скоростей.
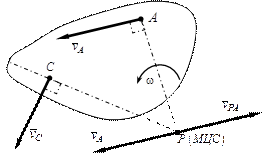
Рис. 1. 13. Мгновенный центр скоростей
Очевидно, если за полюс взять другую точку плоской фигуры, допустим точку С, то, согласно доказанному выше, МЦС. должен находиться на перпендикуляре, проведённом из точки С к скорости этой точки (рис.1.13). Таким образом, МЦС. есть точка пересечения перпендикуляров к скоростям точек плоской фигуры.
Если теперь за полюс принять точку Р, то переносная скорость любой другой точки будет равна нулю. Тогда абсолютная скорость произвольной точки плоской фигуры будет равна её скорости во вращательном движении около МЦС.
Зная положение МЦС и угловую скорость плоской фигуры, можно определить скорость любой точки в данный момент времени так же как определяется скорость точки вращающегося тела. Как уже было сказано, МЦС определяется для данного положения плоской фигуры. В соседнем положении мгновенным центром скоростей является другая точка.
Свойства мгновенного центра скоростей:
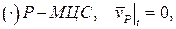 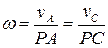
| 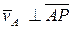 , , 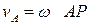 , ,
|
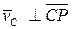 , , 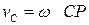 , ,
|
Дата добавления: 2015-08-08; просмотров: 974;
