Сложение ускорений в составном движении

Абсолютное ускорение точки при непоступательном переносном движении равно векторной сумме трех составляющих ускорений — переносного, относительного и ускорения Кориолиса.

По определению ускорение есть производная от скорости по времени

.

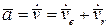Для вычисления производной от относительной скорости 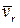применим формулу Бура:

.

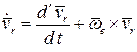Возьмём производную от переносной скорости по времени:

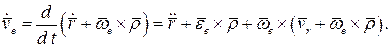
В результате имеем соотношение

.

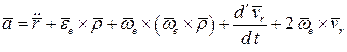Обозначим сумму первых трёх слагаемых через 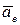. Это ускорение точки подвижной системы координат (переносного тела, участвующего в поступательном и сферическом движении), совпадающей в данный момент времени с исследуемой точкой, т. е. — переносное ускорение:

.

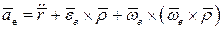Ускорение в относительном движении находится как относительная производная от относительной скорости:

.

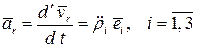Последнее слагаемое основной формулы называется ускорением Кориолиса или поворотным ускорением:

.

Окончательно абсолютное ускорение можно определить как результат сложения переносного, относительного и кориолисова ускорений:

.

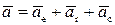Ускорение Кориолиса появляется по следующим причинам:

· из-за изменения переносной скорости в относительном движении (рис.1.9 а),

· из-за изменения относительной скорости в переносном движении (рис.1.9 б).

.

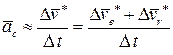Рис. 1. 9. Причины возникновения ускорение Кориолиса

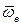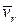Рассмотрим подробней алгоритм вычисления кориолисова ускорения. Из определения векторного произведения следует, что вектор ускорения Кориолиса направлен перпендикулярно векторам — сомножителям и причём вращение первого из них 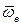производимое по кратчайшему пути ко второму сомножителю 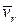должно наблюдаться с острия вектора-результата происходящим в направлении против часовой стрелки.

Модуль ускорения Кориолиса определяется по формуле:

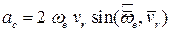
и, следовательно, 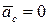в следующих случаях:

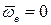
	при переносном поступательном движении;
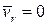
	при относительном покое;
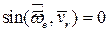
	в том случае, когда угол между векторами относительной скорости и переносной угловой скорости равен 0 или 180 градусов.