Дизъюнкция (логическое сложение)

Дизъюнкция — это такая двоичная функция, которая равна нулю тогда и только тогда, когда все аргументы функции равны нулю, другое определение: дизъюнкция — это такая функция, которая равна единице, если хотя бы один аргумент равен единице.

Функции дизъюнкции соответствует операция логическое сложение. Знак операции: Пример записи формулы функции дизъюнкция: f (х1, х2 ) = =х1 х2. Читается формула так: «х1 или х2».

Запись на языках программирования: «х1 OR х2».

Функцию дизъюнкция реализует логический элемент дизъюнктор (элемент ИЛИ).

Логическое сложение (дизъюнкция) обозначается символом "+" или V (первая буква латинского слова vel-или). Таким образом, логическая сумма равна единице тогда, когда равно единице одно или несколько слагаемых.

В качестве примера реализации функции дизъюнкция рассмотрим схему голосования «хотя бы один». На рис. показана цепь с N кнопками, позволяющими включать индикаторную лампочку. Лампочка засветится в случае, если будет замкнут хотя бы один ключ, то есть схема реализует функцию дизъюнкция.

Дизъюнкцию реализует логическое устройство (вентиль) называемое дизьюнктор (рис. 4.3 a,b,c):

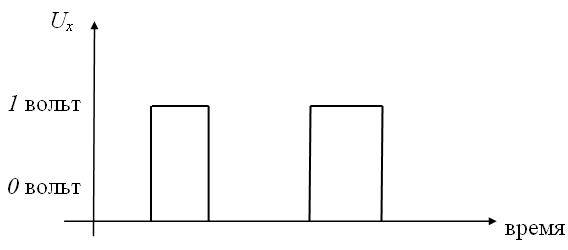
Рис. 4.3a.

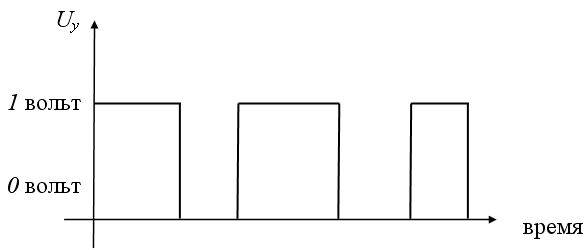
Рис. 4.3b.

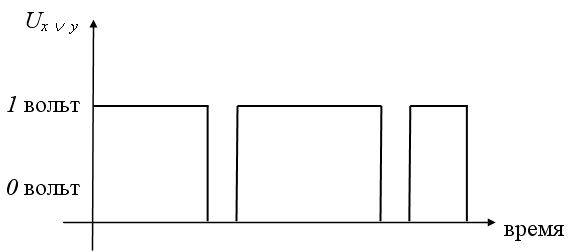
Рис. 4.3c. Принцип работы дизъюнктора

Дизъюнктор условно изображается схематически электрической цепью вида (рис. 4.4)

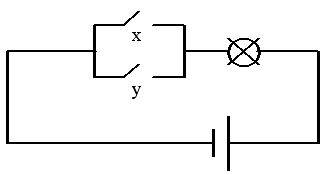
Рис. 4.4. Электрический аналог схемы дизъюнктора

В качестве примера цепи, реализующей: функцию ИЛИ, можно привести параллельное соединение замыкающих контактов нескольких реле. Цепь, в которую входят эти контакты, будет замкнута, если сработает хотя бы одно реле.

Работу дизъюнктора можно интерпретировать и схемой голосования «хотя бы один». На рис. 4.5 показана цепь с двумя (а в общем случае с N) кнопками, позволяющими включать индикаторную лампочку. Лампочка засветится в случае, если будет замкнут хотя бы один ключ, то есть схема реализует функцию дизъюнкция.

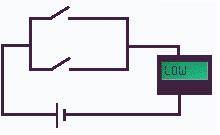
Рис 4.5

Таблица истинности операции логического сложения