Разложение элементарных функций в ряд Маклорена
Найдём разложение основных элементарных функций в ряд Маклорена:
1. 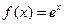
так как 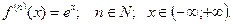 и
и 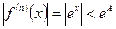 , при
, при 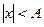 , где А - сколь угодно большое положительное число, следовательно функция
, где А - сколь угодно большое положительное число, следовательно функция 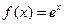 - разложима в ряд Маклорена, сходящийся к ней при
- разложима в ряд Маклорена, сходящийся к ней при 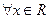 :
:
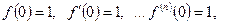
тогда
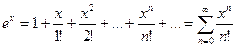 (1)
(1)
Где 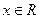
2. 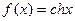
Используя разложение (1), определение 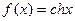 и свойство суммы сходящихся рядов имеем:
и свойство суммы сходящихся рядов имеем:
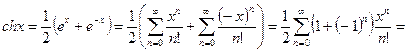
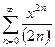 , (2)
, (2)
Где 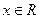 .
.
3. 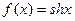
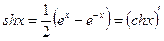
на основании теоремы о почленном дифференцировании степенного ряда получаем:
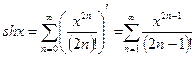 (3)
(3)
Где 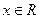 .
.
4. 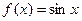
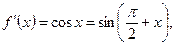
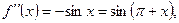
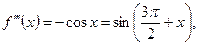
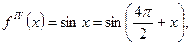
…………………………………
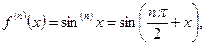
Т.к. 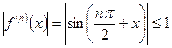 , для
, для 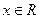 , то функция разложима в ряд Маклорена
, то функция разложима в ряд Маклорена
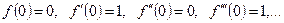
Окончательно получаем
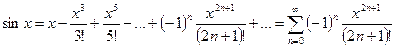 (4)
(4)
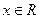
5. 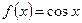
Воспользуемся соотношением 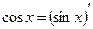 .
.
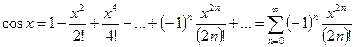 (5)
(5)
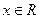
6. 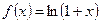
Рассмотрим ряд:
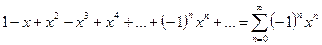
При 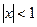 это убывающая геометрическая прогрессия, ее сумма
это убывающая геометрическая прогрессия, ее сумма  .
.
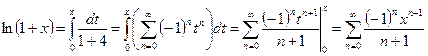 (6)
(6)
Для 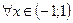 .
.
7. 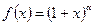 , где aÎR.
, где aÎR.
Заметим, что функция и ее производная 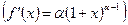 удовлетворяют дифференциальному уравнению
удовлетворяют дифференциальному уравнению
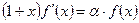 (7)
(7)
с начальными условиями: f(0)=1;
Решение задачи Коши для дифференциального уравнения единственно, следовательно, если найдётся степенной ряд
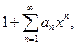
удовлетворяющий уравнению, то он и будет искомым разложением заданной функции.
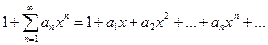
Подставим ряд и его производную в соотношение (7):
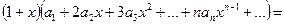
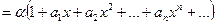
Приведем подобные члены
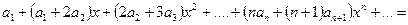

Приравниваем коэффициенты при одинаковых степенях:
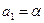 ,
,
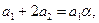
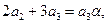
………………………….
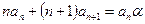
Коэффициент 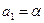 , остальные коэффициенты находим подставляя найденное выражение в нижнюю строчку, т.е.
, остальные коэффициенты находим подставляя найденное выражение в нижнюю строчку, т.е.
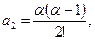
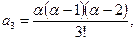
………………………………………..
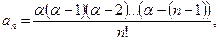
…………………………………………..
Таким образом
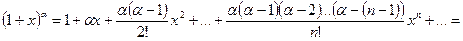
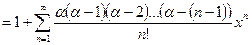
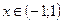 .
.
Ряд, стоящий в правой части равенства, называется биномиальным. При 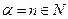 все коэффициенты этого ряда, начиная с (n+1) обращаются в нуль и степенной ряд преобразуется в бином Ньютона
все коэффициенты этого ряда, начиная с (n+1) обращаются в нуль и степенной ряд преобразуется в бином Ньютона
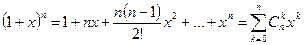
Дата добавления: 2015-08-11; просмотров: 734;
