Неопределенный интеграл и его свойства
Совокупность всех первообразных к функции  называется неопределенным интегралом от функции
называется неопределенным интегралом от функции 
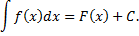
Функция  называется подынтегральной функцией,
называется подынтегральной функцией, 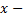 переменной интегрирования.
переменной интегрирования.
Другими словами, неопределенный интеграл – это общая первообразная, содержащая произвольную постоянную, при каждом численном значении которой получается частная первообразная.
Восстановление функции по ее производной (отыскание неопределенного интеграла) называется интегрированием этой функции. Интегрирование – операция обратная дифференцированию.
Из определения неопределенного интеграла вытекают его свойства.
1)Производная неопределенного интеграла равна подынтегральной функции; дифференциал от неопределенного интеграла равен подынтегральному выражению, т.е.
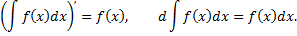
2)Неопределенный интеграл от дифференциала некоторой функции равен сумме этой функции и произвольной постоянной, т.е.

3)Постоянный множитель можно вынести из-под знака интеграла, т.е. если 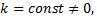 то
то

4)Неопределенный интеграл от алгебраической суммы двух функций равен алгебраической сумме интегралов от этих функций в отдельности, т.е.
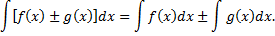
Таблица основных интегралов
Приведем таблицу основных интегралов. Часть формул следует из определения интегрирования как операции, обратной дифференцированию, и таблицы производных. В таблице  произвольная постоянная,
произвольная постоянная, 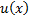 – функция от переменной
– функция от переменной 
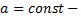 число.
число.
Таблица 6
| Неопределенный интеграл | Первообразная | Неопределенный интеграл | Первообразная |
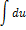
| 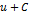
| 
| 
|
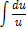
| 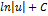
| 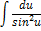
| 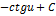
|
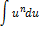
| 
| 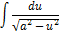
| 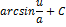
|
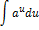
| 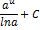
| 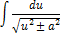
| 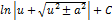
|
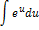
| 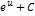
| 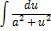
| 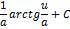
|
| Неопределенный интеграл | Первообразная | Неопределенный интеграл | Первообразная |
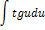
| 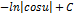
| 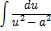
| 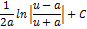
|
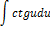
| 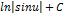
| 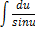
| 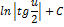
|
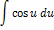
| 
| 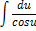
| 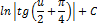
|
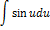
| 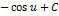
| 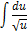
|  + + 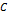
|
Рассмотрим основные методы интегрирования.
Метод непосредственного интегрирования основан на непосредственном использовании формул таблицы интегралов и свойств неопределенного интеграла.
Заметим, что дифференцирование является мощным инструментом проверки результатов интегрирования.
Рассмотрим пример. Требуется найти значение интеграла
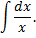
На основе известной формулы дифференцирования
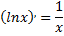
можно сделать вывод, что искомый интеграл равен 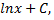 где
где 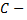 некоторое постоянное число. С другой стороны,
некоторое постоянное число. С другой стороны,
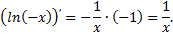
Окончательно можно сделать вывод:
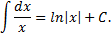
В отличие от дифференцирования, где для нахождения производной использовались четкие приемы и методы, правила нахождения производной, определение производной, для интегрирования такие методы недоступны. При нахождении первообразной следует в основном опираться на знания таблиц производных и первообразных.
Метод непосредственного интегрирования применим только для весьма ограниченных классов функций. Поэтому в большинстве случаев применяются способы, описанные ниже.
Дата добавления: 2015-08-11; просмотров: 3046;
