Первообразная функции
Одной из основных задач дифференциального исчисления является отыскание производной заданной функции. Разнообразные вопросы математического анализа и его многочисленные приложения в механике и технике приводят к обратной задаче: по данной функции  найти такую функцию
найти такую функцию 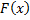 , производная которой была бы равна функции
, производная которой была бы равна функции  , т.е.
, т.е. 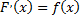 . Восстановление функции по известной производной этой функции – одна из основных задач интегрального исчисления.
. Восстановление функции по известной производной этой функции – одна из основных задач интегрального исчисления.
Функция 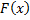 называется первообразной для функции
называется первообразной для функции  на некотором промежутке
на некотором промежутке 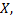 если для всех значений
если для всех значений  из этого промежутка выполняется равенство
из этого промежутка выполняется равенство

Рассмотрим пример. Функция 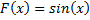 является первообразной для функции
является первообразной для функции  на всей числовой прямой, так как при любом значении переменной
на всей числовой прямой, так как при любом значении переменной 
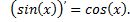
Первообразная у заданной функции не одна. Например,
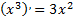 и
и 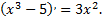
Вообще, если функция  имеет первообразные
имеет первообразные 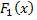 и
и 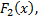 то
то
 т.е.
т.е. 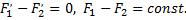
Таким образом, любые две первообразные к одной и той же функции отличаются друг от друга на постоянное слагаемое и чтобы получить все первообразные для данной функции, надо взять какую-нибудь одну и прибавить к ней произвольную постоянную.
Задача отыскания по данной функции  ее первообразной решается неоднозначно. Если функция
ее первообразной решается неоднозначно. Если функция 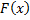 – первообразная для
– первообразная для  , то функция
, то функция
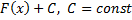 ,
,
также является первообразной для  , так как
, так как
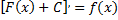
для любого числа 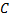 (произвольной постоянной).
(произвольной постоянной).
Дата добавления: 2015-08-11; просмотров: 797;
