Необходимое и достаточное условия экстремума функции двух переменных
Необходимое условие экстремума. Если точка 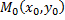 является точкой экстремума функции
является точкой экстремума функции 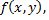 то
то
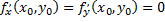
или хотя бы одна из этих производных не существует.
Точки, для которых эти условия выполнены, называются стационарными или критическими. Точки экстремума всегда являются стационарными, но стационарная точка может и не быть точкой экстремума. Чтобы стационарная точка была точкой экстремума, должны выполняться достаточные условия экстремума.
Введем обозначения
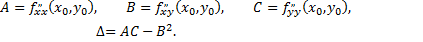
Достаточное условие экстремума. Пусть функция 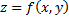 имеет непрерывные частные производные до третьего порядка включительно в некоторой области, содержащей стационарную точку
имеет непрерывные частные производные до третьего порядка включительно в некоторой области, содержащей стационарную точку 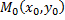 . Тогда:
. Тогда:
1) если 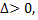 то точка
то точка 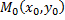 является точкой экстремума для данной функции, причем
является точкой экстремума для данной функции, причем 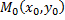 будет точкой максимума при
будет точкой максимума при 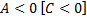 и точкой минимума при
и точкой минимума при 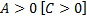 ;
;
2) если 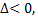 то в точке
то в точке 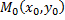 экстремума нет;
экстремума нет;
3) если 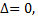 то экстремум может быть, а может и не быть.
то экстремум может быть, а может и не быть.
В третьем случае необходимы дополнительные исследования.
Рассмотрим пример.
Исследовать на экстремум функцию
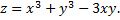
Так как в данном случае 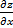 и
и 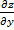 всегда существует, то для нахождения стационарных точек получим систему уравнений
всегда существует, то для нахождения стационарных точек получим систему уравнений
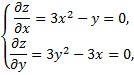
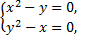
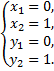
Таким образом, получены две стационарные точки 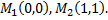
Находим
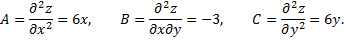
Тогда
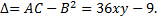
В точке 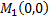 величина
величина 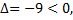 т.е. в этой точке экстремума нет. В точке
т.е. в этой точке экстремума нет. В точке 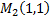 величина
величина

следовательно, в этой точке данная функция достигает локального минимума 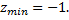
Дифференцируемая функция в ограниченной замкнутой области 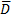 достигает своего наибольшего (наименьшего) значения либо в стационарной точке, лежащей внутри области
достигает своего наибольшего (наименьшего) значения либо в стационарной точке, лежащей внутри области 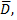 либо на границе этой области. Для отыскания наибольшего и наименьшего значений функции в замкнутой области
либо на границе этой области. Для отыскания наибольшего и наименьшего значений функции в замкнутой области 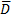 необходимо найти все критические точки, лежащие внутри данной области и на ее границе, вычислить значения функции в этих точках, а также во всех остальных точках границы, а затем путем сравнения полученных чисел выбрать наибольшее и наименьшее из них.
необходимо найти все критические точки, лежащие внутри данной области и на ее границе, вычислить значения функции в этих точках, а также во всех остальных точках границы, а затем путем сравнения полученных чисел выбрать наибольшее и наименьшее из них.
Рассмотрим пример. Найти наибольшее и наименьшее значения функции
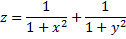
на круге радиуса 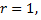 с центром в начале координат
с центром в начале координат 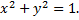
Найдем частные производные функции
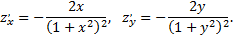
Найдем критические точки функции из системы

решая данную систему, получим  т.е. имеется одна критическая точка
т.е. имеется одна критическая точка 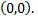
Найдем критические точки функции на границе области – окружности, задаваемой уравнением  Подставляя
Подставляя 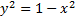 в функцию
в функцию 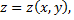 получим функцию одной переменной
получим функцию одной переменной
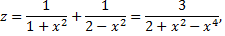
причем 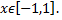
Найдем производную и приравняем ее к нулю, получим критические точки на границе области
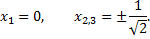
Найдем значения 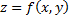 в критических точках внутри области
в критических точках внутри области  и на ее границе
и на ее границе
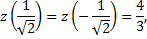
а также на концах отрезка 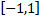 на границе области
на границе области
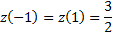
и выбираем среди них наибольшее и наименьшее.
Итак,
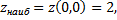

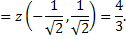
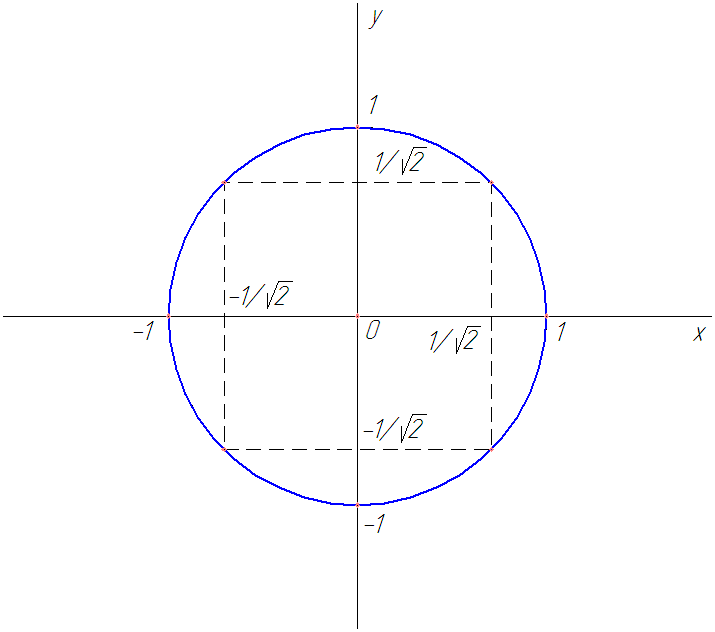
Рис. 35
Замкнутая область
Дата добавления: 2015-08-11; просмотров: 7418;
