Теорема о смешанных производных
Аналогично определяются частные производные третьего и более высоких порядков. Частные производные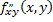 
и 
называются смешанными. Значения смешанных производных равны в тех точках, в которых эти производные непрерывны.
Рассмотрим пример.
Найти частные производные второго порядка функции
Вначале найдем производные первого порядка
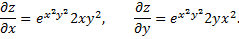
Продифференцируем еще раз
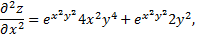
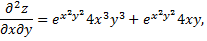
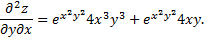
Дата добавления: 2015-08-11; просмотров: 1052;