Общая схема исследования функции и построение ее графика

Чтобы построить график функции 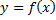, необходимо ее исследовать, т.е. определить характерные особенности графика данной функции. Для этого следует:

1) найти область определения функции;

2) найти точки пересечения графика функции с осями координат;

3) исследовать функцию на четность и нечетность;

4) исследовать функцию на непрерывность: найти точки разрыва и установить характер разрыва;

5) найти асимптоты кривой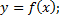

6) найти интервалы возрастания и убывания функции, точки экстремума;

7) найти интервалы выпуклости и вогнутости кривой 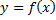и точки ее перегиба;

8) построить график функции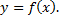

Рассмотрим пример. Построить график функции

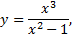
предварительно определив его характерные особенности.

1)Найдем область определения функции:

,

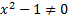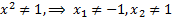
т.е.

2)Найдем точки пересечения графика функции с осями координат:

- пересечение с осью 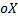: 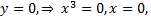т.е. точка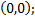

- пересечение с осью 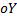: 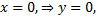т.е. точка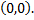

3) Исследуем функцию на четность (нечетность)

- функция нечетная.

4)В точках 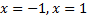функция неопределенна, следовательно, терпит разрыв, определим какого рода

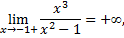
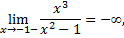
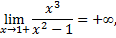
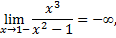
в точках 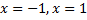функция терпит разрыв второго рода, следовательно

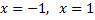
- вертикальные асимптоты.

5) Найдем наклонную асимптоту кривой в виде 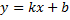, где

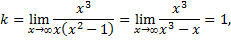
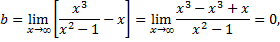
следовательно, – наклонная асимптота.

6) Найдем интервалы возрастания и убывания функции, точки экстремума

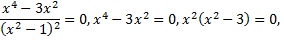
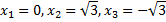
– это критические точки, которые делят область определения на участки возрастания и убывания. Определим знак производной функции на выявленных участках:

следовательно, на промежутке 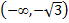функция возрастает;

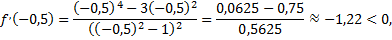
следовательно, на промежутке функция убывает;

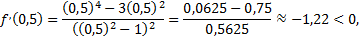
следовательно, на промежутке 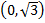функция убывает;

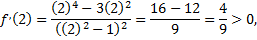
следовательно, на промежутке 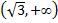функция возрастает;

Таким образом, 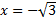– точка максимума, 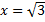– точка минимума.

7)Найдем интервалы выпуклости и вогнутости кривой и точки ее перегиба.

Для этого определим критические точки второго рода

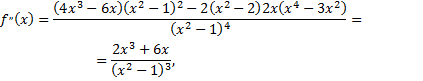
Точка 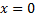– критическая точка второго рода, которая делит область определения функции на участки выпуклости и вогнутости

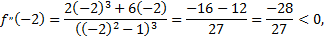
следовательно, на промежутке 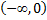данная кривая выпукла;

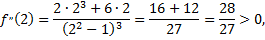
следовательно, на промежутке 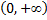данная кривая вогнута.

8)Построим график функции:

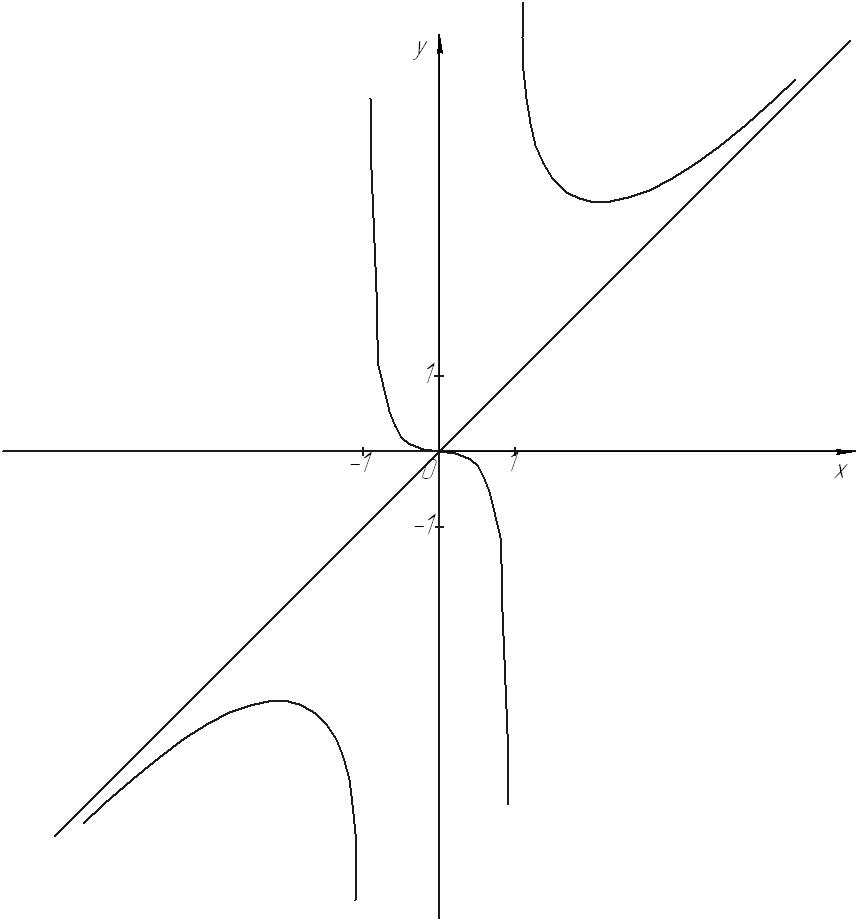
Рис. 33

График функции

Контрольные вопросы

1. Дать определение экстремума функции.

2. Какая функция называется возрастающей (убывающей)?

3. Как найти точки перегиба функции и участки выпуклости и вогнутости функции?

4. Что называют асимптотами графика функции?

5. Дать общую схему исследования функции.