Точки перегиба функции и участки выпуклости и вогнутости графика функции
График функции 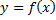 называется выпуклым в интервале
называется выпуклым в интервале 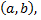 если он расположен ниже касательной, проведенной в любой точке этого интервала.
если он расположен ниже касательной, проведенной в любой точке этого интервала.
График функции 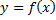 называется вогнутым в интервале
называется вогнутым в интервале 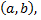 если он расположен выше касательной, проведенной в любой точке этого интервала.
если он расположен выше касательной, проведенной в любой точке этого интервала.
Рис. 32
Участки выпуклости и вогнутости графика функции
Достаточное условие выпуклости (вогнутости) графика функции: если 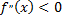 в интервале
в интервале 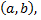 то график функции является выпуклым в этом интервале; если
то график функции является выпуклым в этом интервале; если 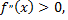 то в интервале
то в интервале 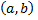 график функции вогнутый.
график функции вогнутый.
Пусть функция  дифференцируема на интервале
дифференцируема на интервале 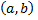 и точка
и точка 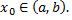 Точка
Точка 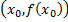 графика функции
графика функции 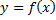 называется точкой перегиба этого графика, если существует такая окрестность точки
называется точкой перегиба этого графика, если существует такая окрестность точки  оси абсцисс, в пределах которой график функции
оси абсцисс, в пределах которой график функции  слева и справа от точки
слева и справа от точки  имеет разные направления выпуклости. Если
имеет разные направления выпуклости. Если  –абсцисса точки перегиба графика функции
–абсцисса точки перегиба графика функции 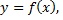 то вторая производная равна нулю или не существует. Точки, в которых
то вторая производная равна нулю или не существует. Точки, в которых 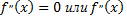 не существует, называются критическими точками второго рода.
не существует, называются критическими точками второго рода.
Если  – критическая точка второго рода и при произвольном достаточно малом
– критическая точка второго рода и при произвольном достаточно малом 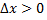 выполняются неравенства
выполняются неравенства
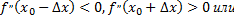
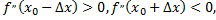
то точка кривой 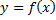 с абсциссой
с абсциссой  является точкой перегиба. Если
является точкой перегиба. Если

имеют одинаковые знаки, то точка кривой 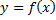 с абсциссой
с абсциссой  не является точкой перегиба.
не является точкой перегиба.
Рассмотрим пример. Найти промежутки выпуклости и вогнутости графика функции

Продифференцируем два раза данную функцию, приравняем к нулю, полученное уравнение решим относительно переменной  получим критические точки второго рода, которые поделят всю область определения функции на участки выпуклости и вогнутости
получим критические точки второго рода, которые поделят всю область определения функции на участки выпуклости и вогнутости
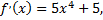
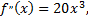
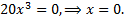
Точка 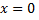 делит всю область определения функции на два участка. Определим знак производной второго порядка на этих участках:
делит всю область определения функции на два участка. Определим знак производной второго порядка на этих участках:
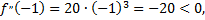
следовательно, данная кривая выпукла на участке 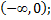
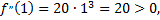
следовательно, данная кривая вогнута на участке 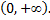
Дата добавления: 2015-08-11; просмотров: 1381;
