Производные и дифференциалы высших порядков

Производная от производной некоторой функции называется производной второго порядка этой функции. Производная от второй производной называется производной третьего порядка и т.д. Производные, начиная со второй, называются производными высших порядков и обозначаются

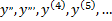
Производные высших порядков имеют широкое применение в физике. Например, если функция 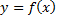описывает закон движения материальной точки по прямой линии, то первая производная 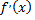есть мгновенная скорость точки в момент времени а вторая производная равна скорости изменения скорости, т.е. ускорению движущейся точки в этот момент.

Рассмотрим дифференциалы высших порядков. Пусть функция дифференцируема в каждой точке некоторого промежутка. Тогда ее дифференциал

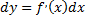
называют дифференциалом первого порядка. Пусть функция 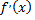дифференцируема в некоторой точке Тогда ее дифференциал

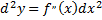
называют дифференциал второго порядка. Для -го дифференциала функции справедлива формула

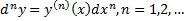
Рассмотрим пример. Вычислим дифференциал 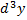функции

.

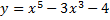Последовательно дифференцируя, получим

Контрольные вопросы

1. Сформулировать теоремы Ферма, Ролля, Лагранжа, Коши.

2. В чем состоит основная идея правила Лопиталя?

3. Дать определение дифференциала функции.

4. Как находятся производные высших порядков?