Экстремум функции. Возрастание и убывание функции
Функция  называется возрастающей в точке
называется возрастающей в точке  если при любом достаточно малом
если при любом достаточно малом 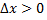 выполняется условие
выполняется условие
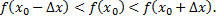
Функция  называется убывающей в точке
называется убывающей в точке  если при любом достаточно малом
если при любом достаточно малом 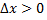 выполняется условие
выполняется условие
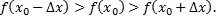
Функция  называется возрастающей в интервале
называется возрастающей в интервале 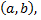 если для любых двух точек
если для любых двух точек 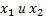 из указанного интервала, удовлетворяющих неравенству
из указанного интервала, удовлетворяющих неравенству 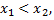 выполняется неравенство
выполняется неравенство
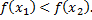
Функция  называется убывающей в интервале
называется убывающей в интервале 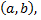 если для любых двух точек
если для любых двух точек 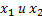 из указанного интервала, удовлетворяющих неравенству
из указанного интервала, удовлетворяющих неравенству 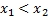 выполняется неравенство
выполняется неравенство
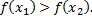
Признаки возрастания и убывания функции:
1) Если 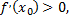 то функция
то функция  возрастает в точке
возрастает в точке 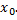
2) Если 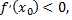 то функция
то функция  убывает в точке
убывает в точке 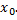
Значение 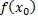 называется максимумом функции
называется максимумом функции  , если при любом достаточно малом
, если при любом достаточно малом 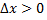 выполняется условие
выполняется условие
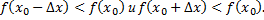
Точка 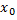 называется в этом случае точкой максимума функции
называется в этом случае точкой максимума функции 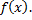
Значение 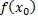 называется минимумом функции
называется минимумом функции 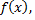 если при любом достаточно малом
если при любом достаточно малом 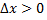 выполняются условия
выполняются условия
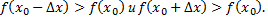
Точка  называется в этом случае точкой минимума функции
называется в этом случае точкой минимума функции 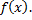
Максимум или минимум функции называется экстремумом функции. Точка максимума или минимума функции называется точкой ее экстремума.
Необходимое условие экстремума: если функция  в точке
в точке  имеет экстремум, то производная
имеет экстремум, то производная 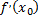 обращается в нуль или не существует.
обращается в нуль или не существует.
Точка  в которой
в которой 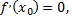 называется стационарной точкой. Точки, в которых
называется стационарной точкой. Точки, в которых
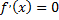
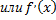 не существует, называются критическими точками. Не всякая критическая точка является точкой экстремума.
не существует, называются критическими точками. Не всякая критическая точка является точкой экстремума.
Достаточное условие экстремума:
1) Если  критическая точка функции
критическая точка функции  и при произвольном достаточно малом
и при произвольном достаточно малом
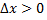 выполняются неравенства
выполняются неравенства
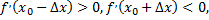
то функция  в точке
в точке  имеет максимум; если же
имеет максимум; если же
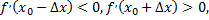
то функция  в точке
в точке  имеет минимум. Если знаки
имеет минимум. Если знаки
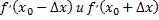
одинаковы, то функция  в точке
в точке  экстремума не имеет.
экстремума не имеет.
2) Если
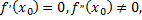
то функция  в точке
в точке  имеет экстремум, а именно максимум, если
имеет экстремум, а именно максимум, если 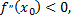 и минимум, если
и минимум, если 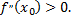
3) Пусть
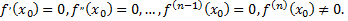
В этом случае функция  имеет в точке
имеет в точке  экстремум, если
экстремум, если 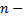 четное число, а именно, максимум при
четное число, а именно, максимум при 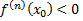 и минимум при
и минимум при  Если
Если 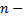 нечетное число, то функция
нечетное число, то функция  в точке
в точке  экстремума не имеет.
экстремума не имеет.
Рассмотрим пример. Найти интервалы возрастания и убывания функции 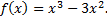
Найдем производную данной функции, приравняем к нулю, полученное уравнение решим относительно переменной  и таким образом определим критические точки, определим знак производной на каждом из участков, разделенных критическими точками
и таким образом определим критические точки, определим знак производной на каждом из участков, разделенных критическими точками
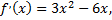
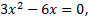


Критические точки  делят область определения функции
делят область определения функции  на участки возрастания и убывания. Определим знак производной функции на этих участках:
на участки возрастания и убывания. Определим знак производной функции на этих участках:
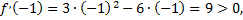
следовательно, на участке 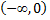 функция
функция 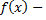 возрастает;
возрастает;
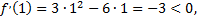
следовательно, на участке 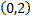 функция
функция 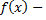 убывает;
убывает;
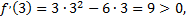
следовательно, на участке  функция
функция 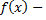 возрастает.
возрастает.
Рассмотрим пример. Исследовать на экстремум функцию
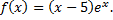
Найдем производную данной функции, приравняем к нулю и решим полученное уравнение относительно переменной  таким образом, получим критические точки, определим, какие из них являются точками экстремума.
таким образом, получим критические точки, определим, какие из них являются точками экстремума.
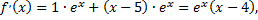
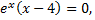
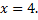
Критическая точка 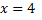 делит всю область определения функции
делит всю область определения функции  на участки возрастания и убывания. Определим знак производной на каждом из участков:
на участки возрастания и убывания. Определим знак производной на каждом из участков:
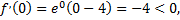
следовательно, на участке 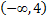 функция
функция 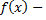 убывает;
убывает;
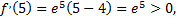
следовательно, на участке 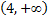 функция
функция 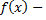 возрастает.
возрастает.
Таким образом, слева от точки 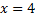 функция
функция  убывает, а справа от точки
убывает, а справа от точки 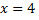 функция
функция  возрастает, согласно первому достаточному условию экстремума можно сделать вывод, что в точке
возрастает, согласно первому достаточному условию экстремума можно сделать вывод, что в точке 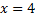 функция имеет минимум
функция имеет минимум
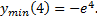
Дата добавления: 2015-08-11; просмотров: 1338;
