Правило Лопиталя. Правило Лопиталя: пусть отношение двух функций при есть неопределенность вида если
Правило Лопиталя: пусть отношение двух функций 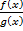 при
при  есть неопределенность вида
есть неопределенность вида 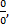 если
если
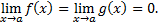
Раскрыть эту неопределенность – значит вычислить предел
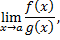
если он существует, или установить, что он не существует.
Теорема Лопиталя устанавливает правило для раскрытия неопределенности вида 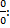 пусть функции
пусть функции  и
и  определены и дифференцируемы в некоторой окрестности точки
определены и дифференцируемы в некоторой окрестности точки  , за исключением самой точки
, за исключением самой точки 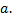 Пусть
Пусть
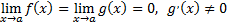
в указанной окрестности точки 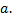 Тогда, если существует предел отношения производных
Тогда, если существует предел отношения производных
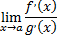
конечный или бесконечный, то существует и предел
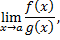
причем справедлива формула
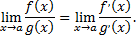
Замечания: 1) если производные 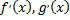 удовлетворяют тем же требованиям, что и сами функции
удовлетворяют тем же требованиям, что и сами функции  и
и  , то правило Лопиталя можно применить повторно:
, то правило Лопиталя можно применить повторно:
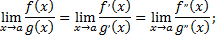
2)правило Лопиталя остается верным и в случае, когда
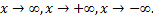
Рассмотрим пример:
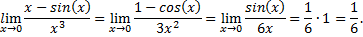

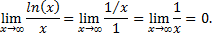
Пусть функция 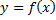 имеет производную в точке
имеет производную в точке 
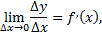
тогда можно записать
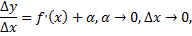
следовательно
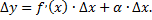
Величина 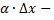 бесконечно малая более высокого порядка, чем
бесконечно малая более высокого порядка, чем 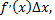 т.е.
т.е. 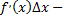 главная часть приращения
главная часть приращения 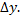
Дата добавления: 2015-08-11; просмотров: 849;
