Дифференцирование неявных функций

Функция называется показательной, если независимая переменная входит в показатель степени, и степенной, если переменная является основанием. Если же и основание, и показатель степени зависят от переменной, то такая функция будет показательно–степенной.

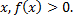Пусть – функции, имеющие производные в точке Найдем производную функции .

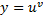Применим способ логарифмического дифференцирования, который состоит в том, что сначала находят логарифмическую производную функции, а затем производную самой функции по формуле

Логарифмируя обе части равенства 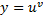, получим

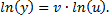
Найдем производную левой и правой части равенства, приняв во внимание, что 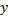–сложная функция

Выразим из полученного равенства 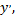учтем, что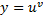

Рассмотрим пример. Найдем производную показательно–степенной функции

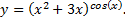
Применим способ логарифмического дифференцирования, в результате чего получим

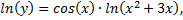
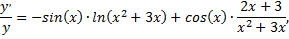
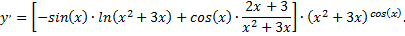
Выше было рассмотрено дифференцирование явных функций, заданных в виде 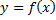. Рассмотрим дифференцирование неявной функции, заданной уравнением

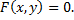
Для нахождения производной функции 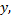заданной неявно, нужно продифференцировать обе части уравнения, рассматривая как функцию от а затем из полученного уравнения найти производную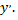

Рассмотрим пример. Найти производную функции, заданной уравнением и вычислить ее значение в точке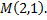

Найдем производную каждого слагаемого, учитывая, что 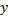–функция от аргумента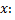

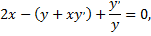
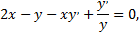
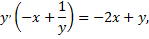
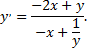
Найдем значение производной в заданной точке:

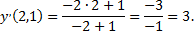
Контрольные вопросы

1. Перечислить правила дифференцирования функций?

2. Как находится производная сложной и неявной функции?

3. В чем состоит геометрический смысл производной?

4. Какие производные применяются для исследования функций и построения их графиков?