Теоремы Ферма, Ролля, Лагранжа, Коши
Теорема Ферма: пусть функция  определена на интервале
определена на интервале 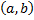 и в некоторой окрестности точке
и в некоторой окрестности точке  этого интервала имеет наибольшее или наименьшее значение. Тогда, если в точке
этого интервала имеет наибольшее или наименьшее значение. Тогда, если в точке  существует производная, то она равна нулю, т.е.
существует производная, то она равна нулю, т.е.
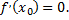
Предположим, что функция  в точке
в точке  имеет наибольшее значение, т.е.
имеет наибольшее значение, т.е.
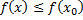
для любого 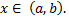 Это значит, что
Это значит, что
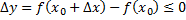
для любой точки 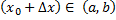 . Поэтому, если
. Поэтому, если

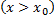 ,
,
то
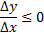
и, следовательно,
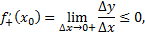
если
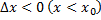 ,
,
то
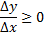
и, следовательно,
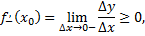
т.е. правая производная в точке  неположительная, а левая – неотрицательная. По условию,
неположительная, а левая – неотрицательная. По условию, 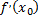 существует и значит,
существует и значит,
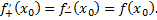
Это возможно только если
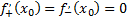 ,
,
но тогда и 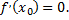
Замечание: теорема неверна, если функцию  рассматривать на отрезке
рассматривать на отрезке  , так как производная на концах отрезка не обращается в нуль.
, так как производная на концах отрезка не обращается в нуль.
Теорема Ролля: пусть на отрезке  определена функция
определена функция 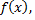 причем:
причем:
1)  непрерывна на отрезке
непрерывна на отрезке 
2)  дифференцируема на интервале
дифференцируема на интервале 
3) 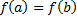 .
.
Тогда существует точка 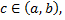 в которой
в которой 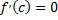 .
.
Так как функция  непрерывна на отрезке
непрерывна на отрезке 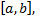 то она имеет на этом отрезке максимальное
то она имеет на этом отрезке максимальное 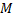 и минимальное
и минимальное 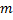 значение, т.е. существуют такие точки
значение, т.е. существуют такие точки 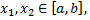 что
что
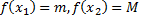
и выполняются неравенства
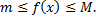
Рассмотрим два случая: 1) 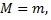 2)
2) 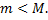
В первом случае 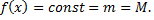 Следовательно, производная
Следовательно, производная  равна нулю в любой точке отрезка
равна нулю в любой точке отрезка 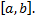
Во втором случае  следовательно, хотя бы одно из двух значений,
следовательно, хотя бы одно из двух значений,  или
или 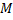 , не принимается на концах отрезка, т.е. существует точка
, не принимается на концах отрезка, т.е. существует точка 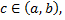 принадлежащая интервалу
принадлежащая интервалу 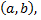 в которой функция
в которой функция  принимает наибольшее или наименьшее значение на интервале
принимает наибольшее или наименьшее значение на интервале 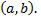 В этом случае, так как
В этом случае, так как  дифференцируема в точке
дифференцируема в точке  то следует, что
то следует, что 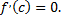
Теорема Лагранжа: пусть на отрезке  определена функция
определена функция 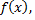 причем:
причем:
1)  непрерывна на отрезке
непрерывна на отрезке 
2)  дифференцируема на интервале
дифференцируема на интервале 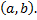
Тогда существует точка 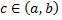 такая, что справедлива формула
такая, что справедлива формула
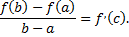
Замечание: величина

является угловым коэффициентом секущей, проходящей через точки 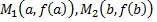 графика функции
графика функции 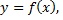 а
а 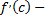 угловой коэффициент касательной к графику в точке
угловой коэффициент касательной к графику в точке 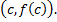
Теорема Коши: пусть функции  и
и 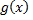 непрерывна на отрезке
непрерывна на отрезке  и дифференцируемы на интервале
и дифференцируемы на интервале 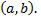 Пусть кроме того,
Пусть кроме того, 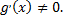 Тогда существует точка
Тогда существует точка 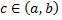 такая, что справедлива формула
такая, что справедлива формула
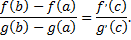
Дата добавления: 2015-08-11; просмотров: 1047;
