Производная обратной, параметрически заданной функции
Пусть функция 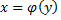 является обратной для функции
является обратной для функции 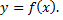 Если функция
Если функция 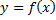 имеет в точке
имеет в точке 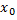 производную
производную 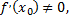 то обратная функция
то обратная функция  также имеет в соответствующей точке
также имеет в соответствующей точке 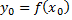 производную, причем
производную, причем
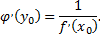
Геометрический смысл производной обратной функции заключается в том, что производная обратной функции 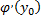 равна тангенсу угла наклона касательной в точке
равна тангенсу угла наклона касательной в точке 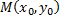 к оси
к оси 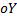

Рассмотрим пример. Найдем производную функции 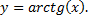 Данная функция является обратной для функции
Данная функция является обратной для функции 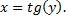
Так как
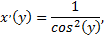
то
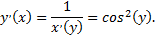
Но

следовательно
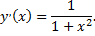
Пусть даны две функции

одной независимой переменной 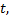 определенные и непрерывные в одном и том же промежутке. Если
определенные и непрерывные в одном и том же промежутке. Если 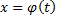 строго монотонна, то обратная к ней функция
строго монотонна, то обратная к ней функция 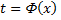 также непрерывна и строго монотонна. Поэтому
также непрерывна и строго монотонна. Поэтому  можно рассматривать как функцию, зависящую от переменной
можно рассматривать как функцию, зависящую от переменной  посредством переменной
посредством переменной 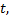 называемой параметром
называемой параметром
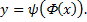
В этом случае говорят, что функция 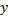 от
от  задана параметрически с помощью уравнений
задана параметрически с помощью уравнений

Предположим, что функции  имеют производные, причем
имеют производные, причем 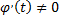 на некотором промежутке, следовательно
на некотором промежутке, следовательно
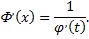
Применим теорему о производной сложной функции
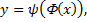
Получим 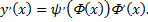 Следовательно
Следовательно
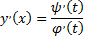
или
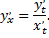
Рассмотрим пример. Найдем производную функции
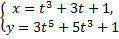 .
.
Применив формулу, получим
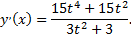
Дата добавления: 2015-08-11; просмотров: 840;
