Определение производной функции. Пусть на некотором промежутке Х определена функция

Пусть на некотором промежутке Х определена функция 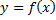. Возьмем любую точку и придадим аргументу в точке произвольное приращение такое, что точка

.

Функция получит приращение

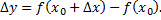
Производной функции в точке называется предел отношения приращения функции в этой точке к приращению аргумента, если он существует

Из определения производной вытекает и способ ее вычисления.

Рассмотрим пример. Найти производную функции 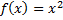в точке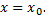

Давая аргументу в точке приращение 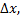найдем соответствующее приращение функции

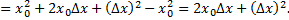
Составим отношение

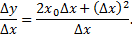
Найдем предел этого отношения при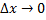

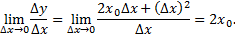
Следовательно, производная функции 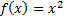в точке 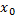равна числу 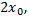это можно записать так