Непрерывность функции в точке и на интервале

Функция называется непрерывной в точке если предел функции и ее значение в этой точке равны, т.е.

Функция называется непрерывной в точке если для любой последовательности значений аргумента 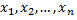сходящейся к 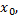последовательность соответствующих значений функций

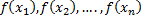
сходится к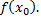

Функция называется непрерывной в точке если для любого существует 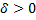такое, что для всех удовлетворяющих неравенству выполняется неравенство