Первый, второй замечательные пределы и их применение к раскрытию неопределенностей. Бесконечно малые и бесконечно большие функции
Первый замечательный предел
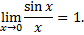
Рассмотрим дугу окружности радиуса 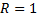 с центральным углом, радианная мера которого равна
с центральным углом, радианная мера которого равна 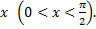
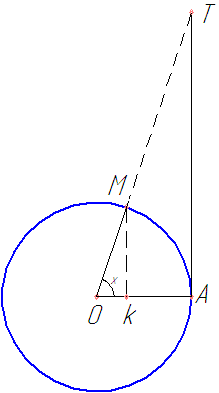
Рис. 30
Дуга окружности
Тогда 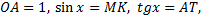
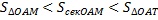
или
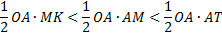
или
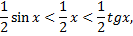
следовательно
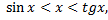
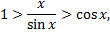
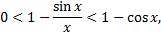
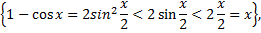

Возьмем любое 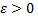 и положим
и положим
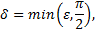
тогда для всех  удовлетворяющих неравенствам
удовлетворяющих неравенствам 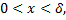 будет выполняться неравенство
будет выполняться неравенство 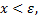 поэтому
поэтому
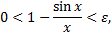

т.е.
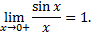
Функция  -четная, так как
-четная, так как
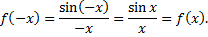
Поэтому и левый предел функции 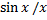 в точке
в точке 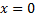 равен единице. Отсюда следует, что
равен единице. Отсюда следует, что
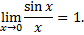
С помощью первого замечательного предела вычисляются многие другие пределы.
Рассмотрим пример. Вычислить предел
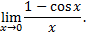
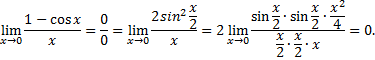
Рассмотрим пример. Вычислить предел
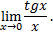
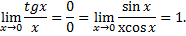
Рассмотрим пример. Вычислить предел
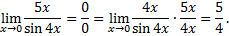
Второй замечательный предел
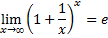
или
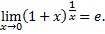
Рассмотрим пример. Вычислить предел

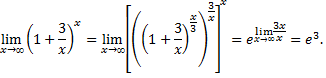
Рассмотрим пример. Вычислить предел
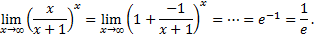
Бесконечно малые функции.
Функция  называется бесконечно малой в точке
называется бесконечно малой в точке 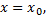 если
если
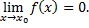
Или функция  называется бесконечно малой в точке
называется бесконечно малой в точке 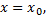 если для любого
если для любого 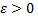 существует
существует 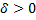 такое, что для всех
такое, что для всех 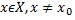 удовлетворяющих неравенству
удовлетворяющих неравенству
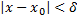
выполняется неравенство 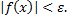
Алгебраическая сумма и произведение конечного числа бесконечно малых функций при 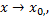 а также произведение бесконечно малой функции на ограниченную функцию являются бесконечно малыми функциями при
а также произведение бесконечно малой функции на ограниченную функцию являются бесконечно малыми функциями при 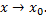
Функция называется бесконечно большой в точке
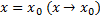
если для любого 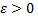 существует
существует 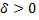 такое, что для всех
такое, что для всех 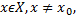 удовлетворяющих неравенству
удовлетворяющих неравенству
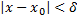
выполняется неравенство 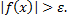
Сумма, разность и произведение бесконечно малых функций являются бесконечно малыми функциями.
Деление бесконечно малой функции на бесконечно малую функцию может привести к различным результатам.
Рассмотрим пример:
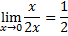
 бесконечно малая функция при
бесконечно малая функция при 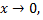
 бесконечно малая функция при
бесконечно малая функция при 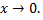
Рассмотрим пример:
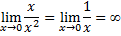
 бесконечно малая при
бесконечно малая при 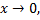
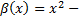 бесконечно малая функция при
бесконечно малая функция при 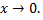
Рассмотрим пример:
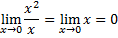
 бесконечно малая при
бесконечно малая при 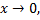
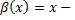 бесконечно малая при
бесконечно малая при 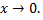
Правила сравнения бесконечно малых функций.
1)Если
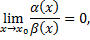
то 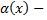 бесконечно малая более высокого порядка, чем
бесконечно малая более высокого порядка, чем 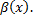
2)Если
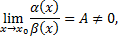
то 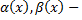 бесконечно малые одного порядка.
бесконечно малые одного порядка.
3)Если
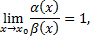
то 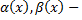 бесконечно малые эквивалентные одного порядка
бесконечно малые эквивалентные одного порядка
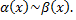
Рассмотрим пример:
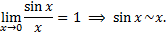
Рассмотрим пример:
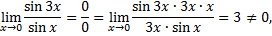
следовательно 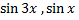 при
при 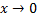 являются бесконечно малыми одного порядка.
являются бесконечно малыми одного порядка.
Дата добавления: 2015-08-11; просмотров: 851;
