Предел функции. Односторонние пределы
Пусть функция  определена на некотором множестве
определена на некотором множестве  и пусть точка
и пусть точка
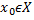 или
или 
Возьмем из  последовательность точек, отличных от
последовательность точек, отличных от 

сходящихся к 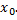 Значения функции в точках этой последовательности также образуют числовую последовательность
Значения функции в точках этой последовательности также образуют числовую последовательность
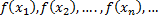
и можно ставить вопрос о существовании ее предела.
Число  называется пределом функции
называется пределом функции  в точке
в точке 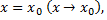 если для любой сходящейся к
если для любой сходящейся к  последовательности
последовательности 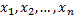 значений аргумента
значений аргумента  отличных от
отличных от  соответствующая последовательность
соответствующая последовательность

значений функции сходится к числу 
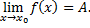
Функция  может иметь в точке
может иметь в точке  только один предел.
только один предел.
Число  называется пределом функции
называется пределом функции  в точке
в точке 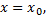 если для любого числа
если для любого числа 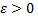 существует число
существует число 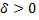 такое, что для всех
такое, что для всех 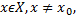 удовлетворяющих неравенству
удовлетворяющих неравенству  выполняется неравенство
выполняется неравенство 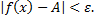
Первое и второе определение предела эквивалентны.
Односторонние пределы.
Число  называется правым (левым) пределом функции
называется правым (левым) пределом функции  в точке
в точке  если для любой сходящейся к
если для любой сходящейся к  последовательности
последовательности
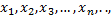
которая больше (меньше)  соответствующая последовательность
соответствующая последовательность
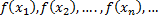
сходится к 
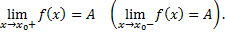
Можно дать другое определение.
Число  называется правым (левым) пределом функции
называется правым (левым) пределом функции  в точке
в точке  , если для любого
, если для любого  существует число
существует число 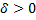 такое, что для всех
такое, что для всех  удовлетворяющих неравенствам
удовлетворяющих неравенствам
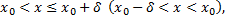
выполняется неравенство 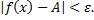
Функция  имеет в точке
имеет в точке  предел тогда и только тогда, когда в этой точке существует как правый, так и левый пределы, и они равны. В этом случае предел функции равен односторонним пределам
предел тогда и только тогда, когда в этой точке существует как правый, так и левый пределы, и они равны. В этом случае предел функции равен односторонним пределам
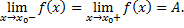
Существует понятие предела при стремлении аргумента к бесконечности.
Число  называется пределом функции
называется пределом функции  при
при 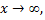 если для любой бесконечно большой последовательности
если для любой бесконечно большой последовательности
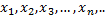
значений аргумента соответствующая последовательность
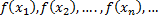
значений функции сходится к 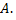
Число  называется пределом функции
называется пределом функции  при
при 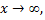 если для любого числа
если для любого числа

существует число 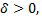 такое, что для всех
такое, что для всех 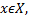 удовлетворяющих неравенству
удовлетворяющих неравенству
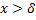
выполняется неравенство
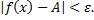
Дата добавления: 2015-08-11; просмотров: 1087;
