Графическое изображение функции. Классификации функций

Наглядно представить поведение функции помогает график функции. Графиком функции 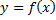называется множество всех точек 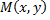плоскости координаты которых связаны данной функциональной зависимостью.

График функции – это линия, уравнением которой служит равенство, определяющее функцию.

Рассмотрим пример. Графиком функции 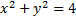является окружность

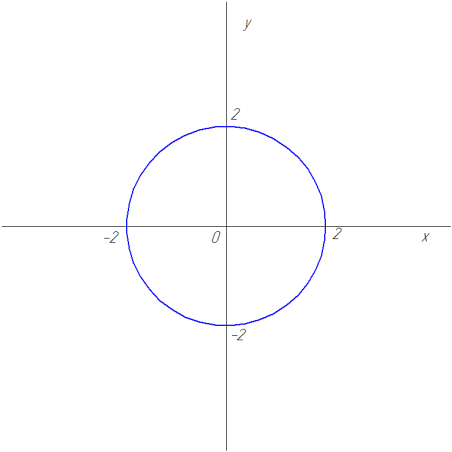
Рис. 25

Окружность

Простейшие функциональные зависимости.

1)Прямая пропорциональная зависимость.

Две переменные величины называются прямо пропорциональными, если при изменении одной из них в некотором отношении другая изменяется в том же отношении. Например, длина окружности и ее радиус, линейное растяжение упругого стержня и нагрузка.

Рассмотрим

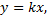
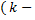коэффициент пропорциональности) – это линейная функция, графиком которой является прямая линия, проходящая через начало координат, с угловым коэффициентом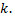

2)Линейная зависимость.

Две переменные 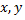связаны линейной зависимостью, если

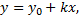
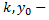постоянные величины. График линейной функции – прямая линия с начальным отрезком 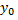и угловым коэффициентом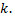

3)Обратная пропорциональная зависимость.

Две переменные величины называются обратно пропорциональными, если при изменении одной из них в некотором отношении, другая изменяется в обратном отношении

Если 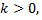то графиком будет равносторонняя гипербола, расположенная в первом и третьем четвертях координатной плоскости .

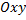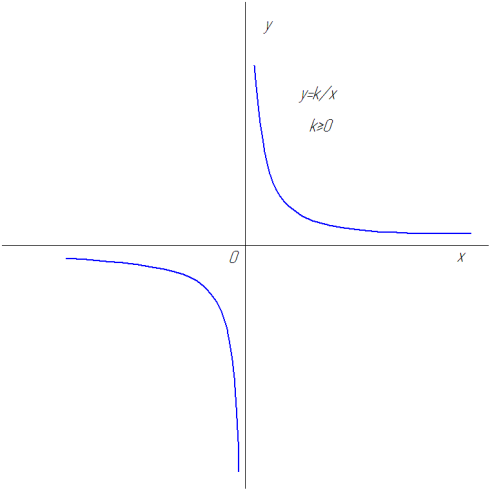
Рис. 26

Равносторонняя гипербола

Если 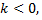то графиком будет равносторонняя гипербола, расположенная во второй и четвертой четвертях координатной плоскости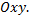

Рис. 27

Равносторонняя гипербола

4)Квадратичная зависимость.

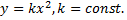
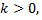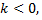График функции – парабола. Если то ветви параболы направлены вверх если то ветви параболы направлены вниз

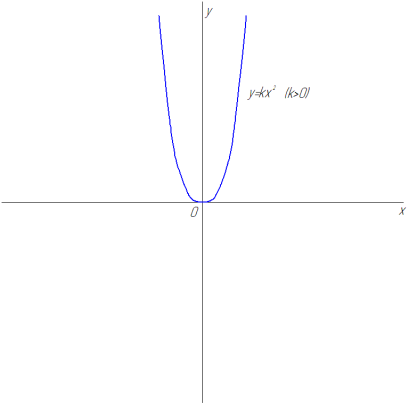
Рис. 28

Парабола

5)Синусоидальная зависимость.

Зависимость, которая используется при изучении периодических процессов

- это называется гармоникой, где амплитуда, 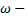частота, 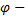начальная фаза.

Периодическая функция с периодом

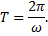
Можно записать в виде

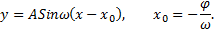
Графиком гармоники будет деформированная синусоида с амплитудой и периодом 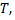сдвинутая вдоль оси 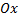на величину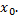

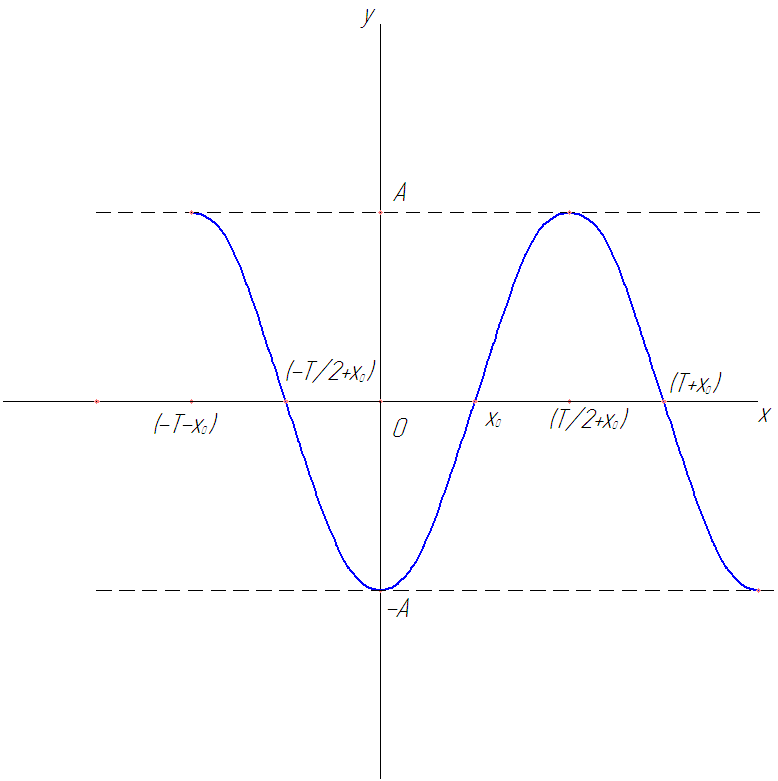
Рис. 29

График гармоники

Понятие обратной функции.

Пусть 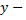функция от аргумента т.е. 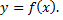Задавая получают соответствующее значение

Если считать 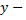аргументом, а 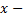функцией, то задают 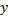и получают соответствующее значение Функция называется обратной по отношению к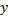

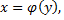
при этом 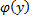должно удовлетворять условию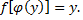

Рассмотрим пример. В формуле объема шара разрешим уравнение относительно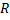

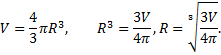
Так получена функция обратная данной.

Рассмотрим пример. Примером обратных функций служат