Определение функции. Функциональная зависимость. Область определения функции и способы ее задания
При изучении закономерностей, встречающихся в природе, все время приходится иметь дело с величинами постоянными и переменными.
Постоянной величиной называется величина, сохраняющая одно и то же значение (параметр).
Переменной величиной называется величина, которая может принимать различные числовые значения.
Например, диаметр окружности может принимать различные значения, т.е. является величиной переменной. Отношение длины окружности к ее диаметру называемое числом 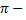 величина постоянная.
величина постоянная.
Изучая какое-нибудь явление, мы имеем дело с совокупностью переменных величин, которые связаны между собой так, что значения одних величин (независимые переменные) полностью определяют значения других (зависимые переменные или функции).
Понятие функции является одним из центральных понятий высшей математики.
Переменная величина  называется функцией от переменной величины
называется функцией от переменной величины  если они связаны между собой так, что каждому рассматриваемому значению величины
если они связаны между собой так, что каждому рассматриваемому значению величины  соответствует единственное вполне определенное значение величины
соответствует единственное вполне определенное значение величины  Это определение впервые сформулировал Н.И. Лобачевский.
Это определение впервые сформулировал Н.И. Лобачевский.
Переменная  называется аргументом или независимой переменной,
называется аргументом или независимой переменной, 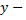 зависимая переменная. Переменные
зависимая переменная. Переменные 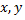 находятся в функциональной зависимости.
находятся в функциональной зависимости.
Область определения (существования) функции – это совокупность всех значений независимой переменной  при которых функция не теряет своего смысла. Часто область определения представляет собой интервал
при которых функция не теряет своего смысла. Часто область определения представляет собой интервал 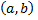 или отрезок
или отрезок 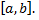
Обозначения 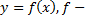 характеристика функции. Частное значение функции
характеристика функции. Частное значение функции 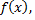 при
при 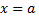 записывается так
записывается так 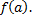
Рассмотрим пример. Найти область определения функции
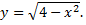
Функция определена, если выполняется неравенство
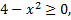

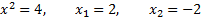
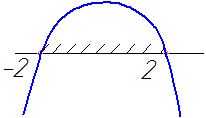
Рис. 24
Следовательно 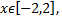 т.е. область определения исследуемой функции есть отрезок.
т.е. область определения исследуемой функции есть отрезок.
Существует несколько способов задания функции.
Аналитический способ, если функция задана формулой вида 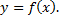 Этот способ наиболее часто встречается на практике. Так, функция
Этот способ наиболее часто встречается на практике. Так, функция 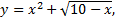 задана аналитически.
задана аналитически.
Не следует путать функцию с ее аналитическим выражением. Например, одна функция

имеет два аналитических выражения: 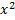 (при
(при 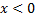 ) и
) и 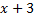 (при
(при 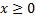 ).
).
Например, формула объема шара – функции от радиуса
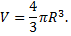
Если функция 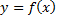 задана формулой, то ее характеристика
задана формулой, то ее характеристика 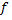 обозначает ту совокупность действий, которую нужно в определенном порядке произвести над значением аргумента
обозначает ту совокупность действий, которую нужно в определенном порядке произвести над значением аргумента  чтобы получить соответствующее значение функции
чтобы получить соответствующее значение функции 
Рассмотрим пример. Дана функция
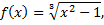
 требуется найти
требуется найти 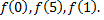
Подставим значение аргумента в функцию
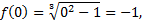
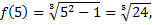
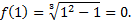
Табличный способ состоит в том, чтофункция задается таблицей, содержащей значения аргумента  и соответствующие значения функции
и соответствующие значения функции 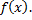
Предположим, что требуется установить зависимость между средней годовой температурой 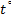 и высотой местности
и высотой местности 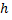 над уровнем моря, выраженной в километрах. В этом случае результаты наблюдений записываются в таблицу (табл.4).
над уровнем моря, выраженной в километрах. В этом случае результаты наблюдений записываются в таблицу (табл.4).
Таблица 4
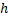
| |||||||||
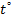
| +7,9 | +4,6 | +0,1 | -5,0 | -10,7 | -16,9 | -23,7 | -30,8 | -38,0 |
Из приведенной таблицы видно, что средняя годовая температура изменяется вместе с высотой местности над уровнем моря. Вывод: средняя годовая температура 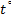 есть функция высоты местности
есть функция высоты местности 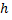 над уровнем моря.
над уровнем моря.
Если функция задана аналитически, то ее всегда можно представить при помощи таблицы.
Графический способ состоит в изображении графика функции – множества точек  плоскости, абсциссы которых есть значения аргумента
плоскости, абсциссы которых есть значения аргумента  а ординаты – соответствующие им значения функции
а ординаты – соответствующие им значения функции 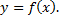
Отсутствие наглядности в аналитическом и табличном способах устраняет графический способ задания функции. Примером графического изображения функции является барограмма (запись самопишущего прибора барографа), дающая графически изменения атмосферного давления со временем.
Словесный способ, если функция описывается правилом ее составления, например, функция Дирихле: 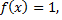 если -рационально;
если -рационально;  если
если  -иррационально.
-иррационально.
Дата добавления: 2015-08-11; просмотров: 1505;
