Расположение поверхностей второго порядка
Преобразование к главным осям имеет целью освободиться от членов, содержащих произведения 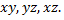 Это достигается поворотом осей, совмещающим их с направлением собственных векторов матрицы
Это достигается поворотом осей, совмещающим их с направлением собственных векторов матрицы

Прежде чем вычислять главные направления, необходимо найти корни характеристического уравнения
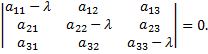
Это уравнение третьей степени относительно 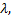 которое имеет три действительных корня
которое имеет три действительных корня  каждому из которых соответствует одно главное направление поверхности, определяемое из уравнений
каждому из которых соответствует одно главное направление поверхности, определяемое из уравнений
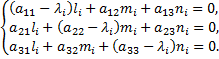
Если все три корня 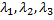 простые и отличны друг от друга, то каждому отвечает единственное инвариантное направление.
простые и отличны друг от друга, то каждому отвечает единственное инвариантное направление.
Координаты собственного вектора 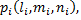 соответствующего собственному значению
соответствующего собственному значению 
Координаты вектора 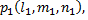 дающего положительное направление оси
дающего положительное направление оси 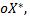 определяются из системы
определяются из системы
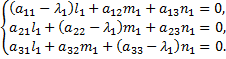
Координаты собственного вектора 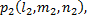 дающего положительное направление оси
дающего положительное направление оси 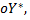 определяются из системы
определяются из системы
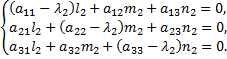
Координаты собственного вектора 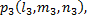 дающего положительное направление оси
дающего положительное направление оси 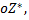 определяются из системы
определяются из системы
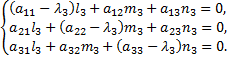
Если два корня равны между собой, но не равны третьему 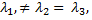 то простому корню
то простому корню  отвечает единственный собственный вектор
отвечает единственный собственный вектор 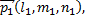 а двойному корню отвечают все направления перпендикулярные к
а двойному корню отвечают все направления перпендикулярные к  Таким образом, достаточно найти два собственных вектора, а третий будет коллинеарен с векторным произведением
Таким образом, достаточно найти два собственных вектора, а третий будет коллинеарен с векторным произведением  Координаты вектора
Координаты вектора 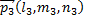 можно взять в виде
можно взять в виде

Если все три корня равны друг другу  то всякий вектор является собственным, и нет необходимости переходить к новой системе координат.
то всякий вектор является собственным, и нет необходимости переходить к новой системе координат.
Если уравнение
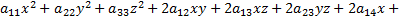
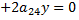
изображает центральную поверхность 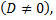 то данное уравнение можно упростить с помощью следующих преобразований.
то данное уравнение можно упростить с помощью следующих преобразований.
1) Начало координат переносят в центр симметрии поверхности 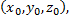 координаты которого определяются из системы уравнений
координаты которого определяются из системы уравнений
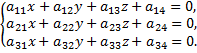
В результате получится уравнение, не содержащее членов с первыми степенями координат
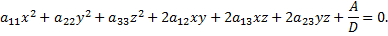
2) Принимают главные оси поверхности за новые оси координат, в результате получают
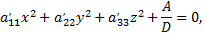
где
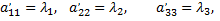
т.е. в уравнении центральной поверхности, отнесенной к главным осям, коэффициентами при квадратах координат служат корни характеристического уравнения, а свободным членом служит отношение дискриминанта уравнения к дискриминанту старших членов.
Если уравнение поверхности изображает параболоид 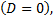 то один из корней характеристического уравнения равен нулю
то один из корней характеристического уравнения равен нулю 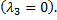 Упрощение уравнения параболоида производится следующим образом: не меняя начало координат, выбирают оси, параллельные главным направлениям, тогда уравнение параболоида принимает вид
Упрощение уравнения параболоида производится следующим образом: не меняя начало координат, выбирают оси, параллельные главным направлениям, тогда уравнение параболоида принимает вид

Выбирают начало координат так, чтобы после переноса начала исчезал свободный член 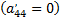 и члены с первыми степенями абсциссы и ординаты
и члены с первыми степенями абсциссы и ординаты 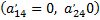 .
.
Тогда уравнение параболоида будет приведено к простейшему виду
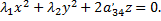
В зависимости от того, имеют ли корни характеристического уравнения  и
и  одинаковые или разные знаки, параболоид будет эллиптическим или гиперболическим.
одинаковые или разные знаки, параболоид будет эллиптическим или гиперболическим.
Контрольные вопросы
1. Что называют инвариантами поверхностей второго порядка?
2. Что называют аффинным преобразованием пространства?
3. Как определить характер места центров симметрии поверхностей второго порядка?
4. Как определяются координаты векторов, дающих положительное направление осей 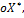
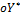 и
и 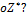
Дата добавления: 2015-08-11; просмотров: 1063;
