Взаимное расположение прямой и плоскости в пространстве

Плоскость, проходящая через точку и через прямую

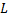
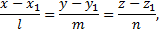
не проходящую через 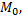представляется уравнением

Рассмотрим пример. Плоскость, проходящая через точку 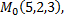и прямую

представляется уравнением

т.е.

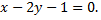
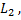Плоскость, проходящая через точку и параллельная данным прямым и представляется уравнением

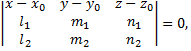
где направляющие коэффициенты данных прямых.

Пусть и 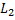– непараллельные прямые. Тогда плоскость, проходящая через прямую и параллельная прямой 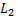представляется уравнением

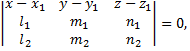
где 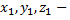координаты точки 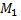прямой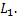

Условие параллельности прямой

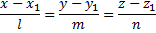
и плоскости

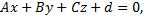
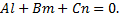
Условие перпендикулярности прямой

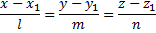
и плоскости

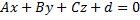
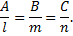
Контрольные вопросы

1. Записать уравнения прямой в пространстве: как пересечение плоскостей; каноническое уравнение прямой, проходящей через две заданные точки. Какой смысл имеют коэффициенты этих уравнений?

2. Как найти угол между прямой и плоскостью?

3. Как найти длину перпендикуляра, опущенного на прямую?