Уравнение прямой в пространстве
Линию в пространстве можно рассматривать как пересечение двух плоскостей и определять заданием двух уравнений первой степени.
Пусть в прямоугольной системе координат  задана произвольная прямая
задана произвольная прямая 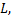 которая получилась в результате пересечения двух плоскостей
которая получилась в результате пересечения двух плоскостей 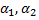 и уравнениями
и уравнениями
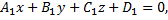
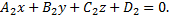
Эти два уравнения определяют прямую 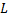 в том случае, если векторы
в том случае, если векторы

не коллинеарны.
Таким образом, система уравнений, состоящая из уравнений двух плоскостей, определяет уравнение прямой в пространстве
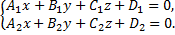
Для решения задач данная система, определяющая прямую в пространстве, является не всегда удобным представлением прямой. В этом случае используют специальный вид уравнений прямой.
Пусть дана прямая 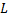 и ненулевой вектор
и ненулевой вектор 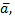 лежащий на данной прямой или параллельный ей. Вектор
лежащий на данной прямой или параллельный ей. Вектор 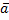 называется направляющим вектором данной прямой.
называется направляющим вектором данной прямой.
Запишем уравнение прямой, проходящей через точку 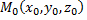 и имеющей направляющий вектор
и имеющей направляющий вектор 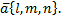 Точка
Точка 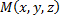 лежит на прямой
лежит на прямой  тогда и только тогда, когда вектор
тогда и только тогда, когда вектор  коллинеарен направляющему вектору
коллинеарен направляющему вектору 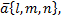 т.е. когда координаты этих векторов пропорциональны
т.е. когда координаты этих векторов пропорциональны

- это есть каноническое уравнение прямой.
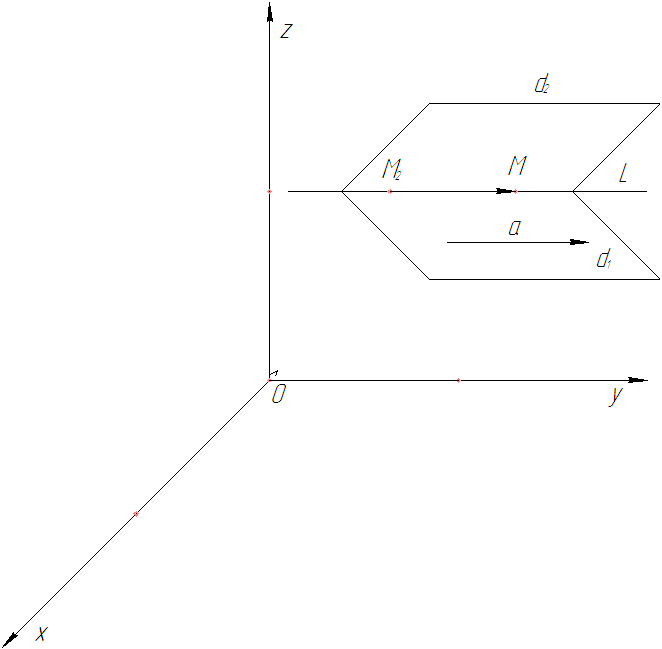
Рис. 23
Линия в пространстве
Чтобы перейти от уравнения

к уравнению
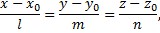
необходимо:
1) найти 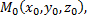 которая принадлежит
которая принадлежит 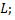 для этого следует задать числовое значение одной из переменных
для этого следует задать числовое значение одной из переменных 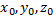 и подставить его вместо соответствующей переменной в уравнение
и подставить его вместо соответствующей переменной в уравнение
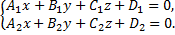
решив систему определить две другие координаты;
2) найти направляющий вектор 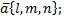 так как прямая
так как прямая 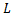 определена пересечением плоскостей
определена пересечением плоскостей  и
и 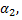 то она перпендикулярна векторам
то она перпендикулярна векторам 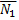 и
и 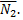 Поэтому вектор
Поэтому вектор 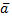 можно взять как
можно взять как
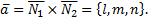
Рассмотрим пример. Записать каноническое уравнение прямой
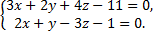
Пусть  тогда
тогда
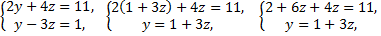
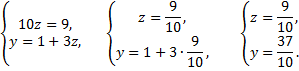
Следовательно
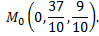
Так как

то направляющий вектор прямой
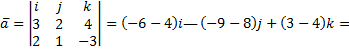


Запишем уравнение заданной прямой в каноническом виде
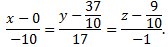
Иногда прямую полезно задавать в параметрическом виде. Например, в тех случаях, когда требуется найти точку пересечения прямой с плоскостью.
Каждое из отношений
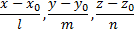
равно частному от деления вектора
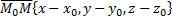
на коллинеарный вектор 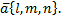 Обозначим это частное через
Обозначим это частное через 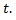 Тогда
Тогда
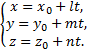
Эти уравнения называются параметрическими уравнениями прямой. Когда величина 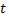 (параметр) принимает различные значения, точка
(параметр) принимает различные значения, точка 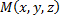 движется по прямой, при
движется по прямой, при 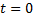 она совпадает с
она совпадает с 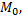 положительным и отрицательным значениям
положительным и отрицательным значениям 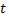 отвечают точки, расположенные на прямой по разные стороны от
отвечают точки, расположенные на прямой по разные стороны от 
Для определения точки пересечения прямой и плоскости следует задать прямую в параметрическом виде и переменные  выраженные через параметр, подставить в уравнение плоскости. Получим уравнение с одной переменной
выраженные через параметр, подставить в уравнение плоскости. Получим уравнение с одной переменной 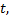 найдем ее. Вернемся к параметрическому виду прямой и найдем
найдем ее. Вернемся к параметрическому виду прямой и найдем 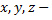 координаты точки пересечения прямой и плоскости.
координаты точки пересечения прямой и плоскости.
Рассмотрим пример. Найдем точку пересечения прямой
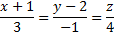
и плоскости
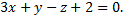
Зададим прямую в параметрическом виде
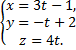 ,
,
Подставим 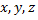 в уравнение плоскости
в уравнение плоскости
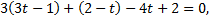
из данного уравнения выразим параметр 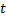
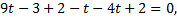
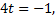

Вернемся к параметрическому уравнению прямой и найдем значения 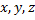
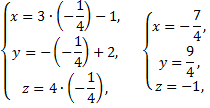
т.е.

Дата добавления: 2015-08-11; просмотров: 1147;
