Условия параллельности и перпендикулярности, прямых в пространстве
Угол между прямыми.
При любом расположении прямых  и
и 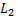 в пространстве, один из двух углов между ними равен углу
в пространстве, один из двух углов между ними равен углу 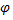 между их направляющими векторами
между их направляющими векторами 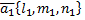 и
и 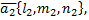 а второй угол равен
а второй угол равен 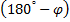
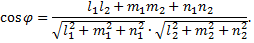
Условие параллельности прямых.
Прямые  и
и 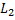 параллельны в том случае, когда их направляющие векторы
параллельны в том случае, когда их направляющие векторы 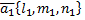 и
и  коллинеарны, следовательно, условием параллельности двух прямых является равенство
коллинеарны, следовательно, условием параллельности двух прямых является равенство
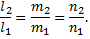
Условие перпендикулярности двух прямых.
Прямые  и
и 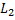 перпендикулярны в том случае, когда их направляющие векторы
перпендикулярны в том случае, когда их направляющие векторы  и
и 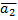 перпендикулярны, т.е.
перпендикулярны, т.е.
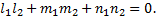
Уравнение перпендикуляра, опущенного из данной точки на данную прямую.
Перпендикуляр, опущенный из точки  на прямую
на прямую 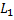

не проходящую через точку 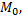 представляется уравнениями
представляется уравнениями
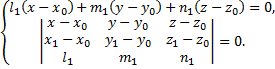
Рассмотрим пример. Найти уравнение перпендикуляра, опущенного из точки 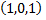 на прямую
на прямую
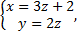
и основание перпендикуляра.
Запишем уравнение прямой в симметричном виде. Пусть точка, принадлежащая прямой, имеет координату 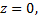 тогда
тогда

Уравнение прямой примет вид
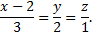
Искомый перпендикуляр представляется уравнениями

После упрощений, получим
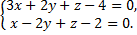
Координаты основания перпендикуляра найдем, решив систему трех уравнений

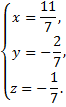
Длина перпендикуляра, опущенного из данной точки на прямую.
Даны точка  и прямая
и прямая 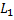
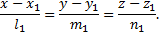
Требуется найти расстояние от точки 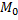 до прямой
до прямой 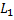 , т.е. длину перпендикуляра, опущенного из точки на прямую.
, т.е. длину перпендикуляра, опущенного из точки на прямую.
Можно пойти по двум путям. Согласно первому пути, можно сначала найти основание перпендикуляра – точку 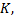 затем длину отрезка
затем длину отрезка 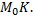 Второй способ основан на применении формулы
Второй способ основан на применении формулы
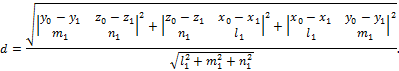
Рассмотрим пример. Найти длину перпендикуляра, опущенного из точки 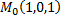 на прямую
на прямую
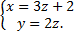
Запишем уравнение прямой в каноническом виде
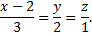
Тогда, согласно данным задачи
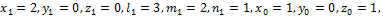
получим
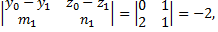
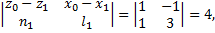
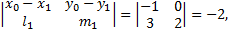
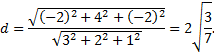
Дата добавления: 2015-08-11; просмотров: 1387;
