Нормальное уравнение плоскости
Нормальное уравнение плоскости.
Рассмотрим произвольную плоскость 
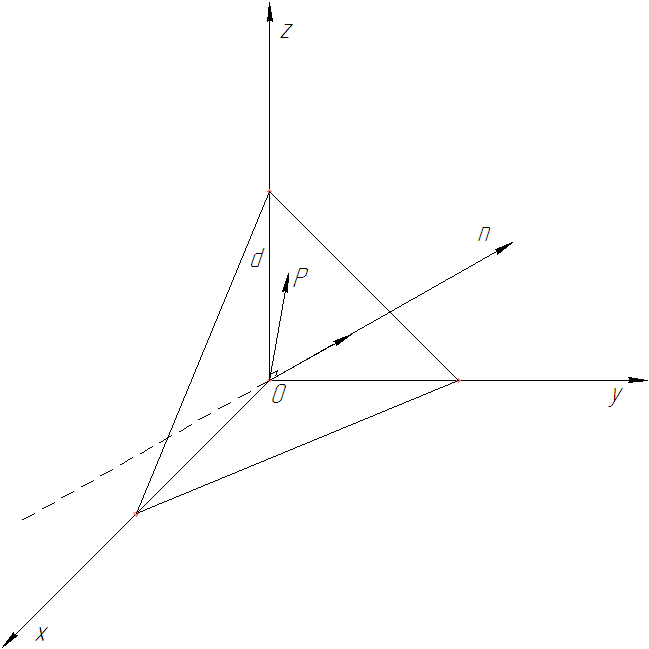
Рис. 22
Плоскость
Проведем через начало координат прямую, перпендикулярную плоскости  данную прямую называют нормалью. Точка
данную прямую называют нормалью. Точка 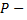 точка пересечения нормали и плоскости
точка пересечения нормали и плоскости 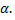 Введем направление от точки
Введем направление от точки 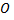 к точке
к точке 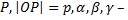 углы между нормалью и осями координат;
углы между нормалью и осями координат; 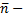 единичный вектор нормали
единичный вектор нормали
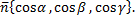
Пусть точка  произвольная точка, которая принадлежит плоскости
произвольная точка, которая принадлежит плоскости  тогда и только тогда, когда
тогда и только тогда, когда 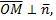 то есть
то есть 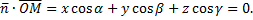
Уравнение всякой плоскости может быть записано в виде
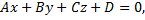
где нормальный вектор плоскости
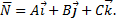
Для приведения данной плоскости к нормальному виду надо все члены уравнения умножить на нормирующий множитель

Знак 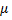 зависит от знака
зависит от знака 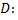 если
если 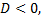 то
то 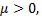 если
если
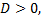 то
то 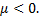
Расстояние от произвольной точки до плоскости.
Пусть имеется точка 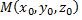 и плоскость
и плоскость 
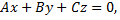
тогда расстояние от точки до плоскости находится по формуле
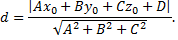
Уравнение плоскости в отрезках.
Если в общем уравнении плоскости 
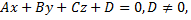
разделить все члены уравнения на 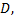 то получим уравнение плоскости
то получим уравнение плоскости  в отрезках
в отрезках
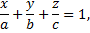
где 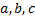 - отсекаемые на осях отрезки.
- отсекаемые на осях отрезки.
Уравнение плоскости, проходящей через три заданные точки
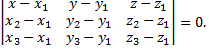
Рассмотрим пример. Найти уравнение плоскости, проходящей через точки 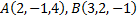 перпендикулярно плоскости
перпендикулярно плоскости 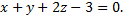


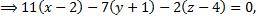
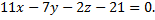
Контрольные вопросы
1. Дать определение уравнения поверхности в ортогональной системе координат.
2. Записать уравнения плоскости: общее, в отрезках на осях, через три заданные точки. Пояснить их смысл.
3. Как найти угол между плоскостями?
4. Как привести уравнение плоскости к нормальному виду?
Дата добавления: 2015-08-11; просмотров: 924;
