Сходимость числовых последовательностей

Сходящаяся последовательность – это последовательность элементов множества 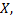имеющая предел в этом множестве.

Расходящаяся последовательность – это последовательность, не являющаяся сходящейся.

Свойства сходящихся последовательностей.

1) Всякая бесконечно малая последовательность является сходящейся. Ее предел равен нулю.

2) Удаление любого конечного числа элементов из бесконечной последовательности не влияет ни на сходимость, ни на предел этой последовательности.

3) Любая сходящаяся последовательность ограничена. Однако не любая ограниченная последовательность сходится.

4) Последовательность сходится тогда и только тогда, когда она является ограниченной и при этом ее верхний и нижний пределы совпадают.

5) Если последовательность 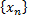сходится, но не является бесконечно малой, то, начиная с некоторого номера, определена последовательность

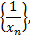
которая является ограниченной.

6)Сумма сходящихся последовательностей также является сходящейся последовательностью.

7)Разность сходящихся последовательностей также является сходящейся последовательностью.

8)Произведение сходящихся последовательностей также является сходящейся последовательностью.

9)Частное двух сходящихся последовательностей определено, начиная с некоторого элемента, если только вторая последовательность не является бесконечно малой. Если частное двух сходящихся последовательностей определено, то оно представляет собой сходящуюся последовательность.

10)Если сходящаяся последовательность ограничена сверху, то ее предел не превышает ни одной из ее верхних граней.

11)Если сходящаяся последовательность ограничена снизу, то никакая из ее нижних граней не превышает ее предела.

12)Если все элементы некоторой последовательности, начиная с некоторого номера, лежат на отрезке между соответствующими элементами двух других сходящихся к одному и тому же пределу последовательностей, то и эта последовательность также сходится к такому же пределу.