Критерий Коши сходимости числовых рядов.
Основным вопросом исследования рядов является вопрос об исследовании их сходимости. Предварительно укажем необходимые и достаточные условия сходимости числовой последовательности.
| Критерии Коши сходимости ч.п. | Для того, чтобы ч.п. 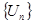 была сходящейся необходимо и достаточно, чтобы для была сходящейся необходимо и достаточно, чтобы для 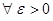 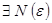 , что для всех n > N , что для всех n > N  и любом целом p >0 выполнялось и любом целом p >0 выполнялось 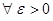 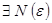 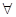 n >N n >N  и и 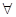 p p 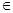 N N 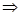 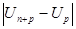 < < 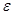
|
| Критерий Коши сходимости числового ряда | Для того, чтобы ч.р. (1) был сходящимся 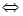 , чтобы для , чтобы для 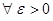 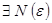 что при n > N что при n > N  и любом целом p >0 выполнялось неравенство: и любом целом p >0 выполнялось неравенство:
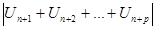 = = 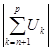 < < 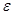 т.е.
т.е. 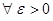 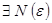 >0 >0 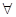 n >N n >N  p – цел. (p>0): p – цел. (p>0):
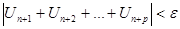
|
Доказательство:
Применив критерий коши для последовательности частичных сумм 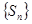 ряда и учтя, что
ряда и учтя, что
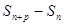 =
= 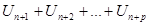 ,
,
получим доказываемый критерий Коши для ряда:
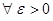
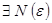
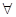 n >N
n >N 
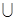
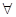 p (p
p (p 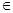 N)
N) 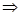
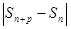 <
< 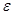
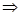
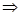
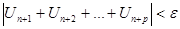 .
.
Дата добавления: 2015-08-14; просмотров: 946;
