Алгебраический критерий устойчивости Гурвица (2 стр. 24-25)
Теорема Гурвица гласит: все корни уравнения
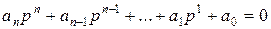
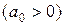
будут иметь отрицательные действительные части тогда и только тогда, когда все диагональные определители главного определителя положительны.
Главный определитель определяется следующим образом:
1. По главной диагонали в порядке возрастания индексов выписываются все коэффициенты от а1 до аn.
2. Каждая из строк дополняется влево коэффициентами с убывающими индексами, вправо – с возрастающими.
3. На месте отсутствующих коэффициентов ставятся нули.
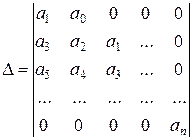
Таким образом, условием устойчивости (отрицательности действительных частей корней) по критерию Гурвица являются:
1. Все коэффициенты характеристического уравнения должны быть положительны – необходимое условие.
2. Все диагональные определители должны быть >0 – достаточное условие, то есть:

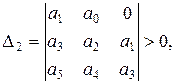
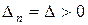
Рассмотрим примеры:
1. Установить, устойчива ли система, если характеристическое уравнение её имеет вид:
а) 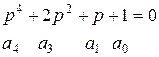 - так как коэффициент а3 = 0, то есть, не выполнено необходимое условие, то система неустойчива.
- так как коэффициент а3 = 0, то есть, не выполнено необходимое условие, то система неустойчива.
б) 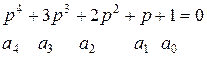 -
- 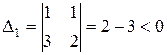 - система не устойчива.
- система не устойчива.
2. Определить, при каких k система будет устойчива:
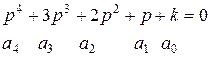
а) 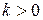
б) 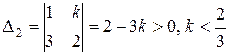
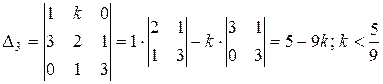 ;
;
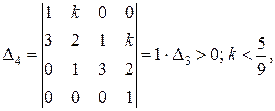 итак
итак 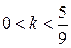 .
.
Область значения параметра, при котором САР устойчива, называют областью устойчивости САР по этому параметру.
Существенные недостатки критерия Гурвица:
1. Критерий лишен наглядности, носит формальный характер и ничего не говорит о качестве устойчивости, то есть насколько далека система от границы устойчивости.
2. Коэффициенты или параметры, характеризующие физические свойства звеньев системы, входят зачастую в столь сложных комбинациях, что практически трудно установить, какие именно параметры и каких звеньев следует изменить, чтобы обеспечить устойчивость САР.
3. Необходимо иметь аналитические уравнения звеньев и всей системы, что не всегда удобно.
Дата добавления: 2015-07-30; просмотров: 1021;
