Алгебраические критерии устойчивости

Раусом и Гурвицем были получены решения задачи устойчивости в несколько различных видах.

Раус опубликовал свое решение в 1875 г. в виде получившей известность таблицы Рауса. Гурвицем был опубликован крите­рий устойчивости в 1895 г. в виде системы определителей. Оба эти критерия приводят к одним и тем же алгебраическим нера­венствам и по существу отличаются только общей формой полу­чения их. Поэтому эти критерии часто объединяют, называя критерием Рауса-Гурвица.

Критерий Рауса. Пусть дано характеристическое урав­нение системы

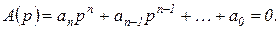(2.1.8)

Составим табл. …, называемую таблицей Рауса.

Таблица 1 - Таблица Рауса

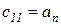
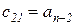
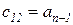
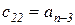
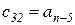
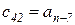
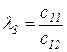
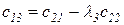
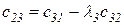
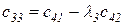
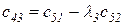
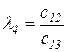
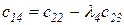
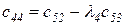
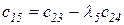
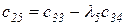
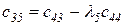
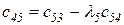
Любой коэффициент таблицы Рауса c_ki при 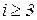(k обозначает номер столбца, а i — номер строки таб­лицы) можно найти по формуле

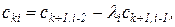(2.1.9)

где

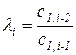при

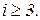
Число строк таблицы Рауса равно степени уравнения плюс единица, т.е. 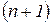. Коэффициентам с отрицательными индексами соответствуют нули.

Критерий устойчивости Рауса формулируется следующим образом. Для того чтобы система была устойчива, не­обходимо и достаточно, чтобы коэффициенты первого столбца таблицы Рауса были положительны, т.е.

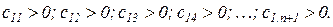(2.1.10)

При составлении таблицы Рауса для численно заданных коэффициентов уравнения можно в целях упрощения вычисле­ний умножать или делить строки таблицы на положительную величину. Это не меняет результат.

Если не все коэффициенты первого столбца положительны, т.е. система неустойчива, то число корней уравнения, лежа­щих в правой полуплоскости, равно числу перемен знаков в первом столбце таблицы.

Критерий Гурвица. Пусть дано характеристическое уравнение системы (2.1.7). Составим таблицу коэффициентов, называемую таблицей Гурвица.

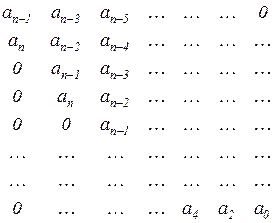
Первая строка образуется из коэффициентов уравнения с индексами 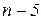и т.д. Вторая строка — из коэффи­циентов уравнения с индексами п,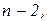 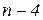и т.д. Каждая последующая строка образуется коэффициентами уравнения с индексами на единицу больше индексов коэффициентов пред­шествующей строки; при этом коэффициенты с индексами меньше нуля и больше п заменяются нулями. Таблица содер­жит п строк, где n — степень уравнения.

Из таблицы Гурвица составляются определители k-го по­рядка D_k отчёркиванием в таблице k строк и k столбцов

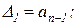
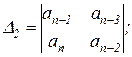
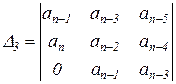(2.1.11)

и т.д.

Эти определители называются определителями Гурвица.

Критерий устойчивости Гурвица формулируется следующим образом. Система устойчива, если 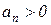и все определи­тели Гурвица больше нуля, т.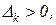е. где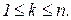

Рассмотрим более подробно случаи, когда :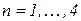

1)

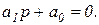
Условия устойчивости:

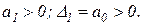(2.1.12)

2)

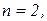
Условия устойчивости:

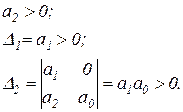(2.1.13)

Последнее условие, при наличии предшествующего, экви­валентно условию .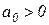

Таким образом, условия устойчивости для уравнения второй степени сводятся к требованиям:

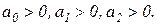(2.1.14)

3)

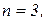
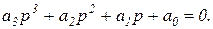
Условия устойчивости:

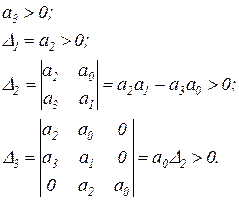(2.1.15)

Последнее условие, при наличии предшествующего, экви­валентно условию .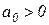

Условие 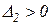при 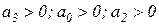возможно лишь при .

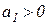Таким образом, условия устойчивости для уравнения третьей степени сводятся к требованиям:

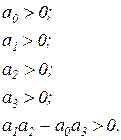(2.1.16)

4)

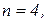
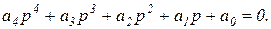
Условия устойчивости:

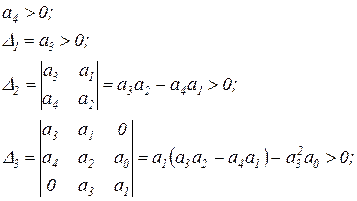
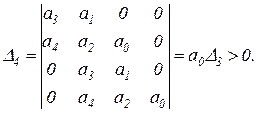
Последнее условие, при наличии предшествующего, экви­валентно условию .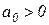

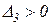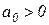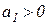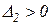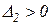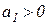Условие при возможно только при и . Условие при , и 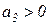возможно при .

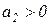Таким образом, условия устойчивости для уравнения чет­вертой степени сводятся к требованиям:

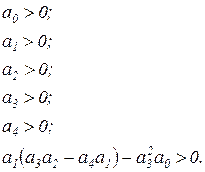(2.1.17)

Из сказанного следует, что условия устойчивости для уравнений первой и второй степени сводятся к требо­ванию положительности коэффициентов характеристи­ческого уравнения.

Для уравнений третьей и четвертой степени, помимо поло­жительности коэффициентов характеристического уравнения, необходимо соблюдение неравенств (2.1.16) и (2.1.17).

При 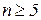число подобных дополнительных неравенств воз­растает, поэтому критерий устойчивости Гурвица рационально использовать при .

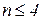Из структуры построения определителей Гурвица следует; что

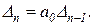(2.1.18)

Согласно критерию устойчивости Гурвица, система устой­чива, если все определители Гурвица больше нуля и, в част­ности, .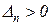

Система находится на границе устойчивости, когда

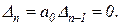(2.1.19)

Это равенство возможно в двух случаях: 1) 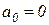и 2) .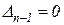

В первом случае говорят, что система находится на границе апериодической устойчивости (один из корней характеристиче­ского уравнения равен нулю).

Во втором случае говорят, что система находится на гра­нице колебательной устойчивости (два сопряженных корня характеристического уравнения находятся на мнимой оси).

В большинстве случаев 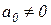и, следовательно, если система находится на границе устойчивости, то это граница колебательной устойчивости.