Преобразование структурных схем

Рассмотрим три элемента структурной схемы: узел разветвления, суммирующий узел и звено, преобразующее сигнал.

Для различных схем соединения введем понятие направле­ния ветвления, указывающее направление разделения сигнала на составляющие или направление его передачи по нескольким ветвям (разветвления). Направление ветвления может или со­ответствовать, или быть противоположным направлению пере­дачи сигнала. В суммирующем узле направление ветвления про­тивоположно направлению передачи сигнала, а в узле разветв­ления — совпадает с направлением передачи сигнала. На рисунке 1.8.4 показаны узел разветвления (а) и суммирующий узел (б), двумя различными стрелками показаны направление передачи сигнала (зачернённая стрелка) и направление ветвления (неза­чернённая стрелка).

Направление ветвления является понятием, применимым как при передаче сигналов, так и при передаче вещества. Нагляд­ным примером рассмотрения направления ветвления при пере­даче вещества может служить обтекание потоком жидкости те­ла с двух сторон (рисунок 1.8.4, в). Здесь направление ветвления вы­ше обтекаемого тела (область 1) направлено по течению жид­кости, а ниже обтекаемого тела (область 2) — против течения жидкости.

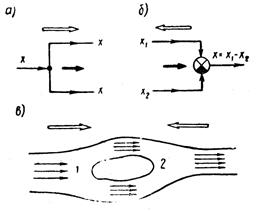
Рисунок 1.8.4 – Примеры разветвлений

Рассмотрим два вида преобразования схем:

а) перемещение суммирующего узла через узел разветвления;

б) перемещение звена через узел.

Правила преобразования схем при каждом из этих видов перемещения существенно зависят от, того, совпадает ли на­правление перемещения с направлением ветвления или они противоположны.

Перемещение суммирующего узла через узел разветвления. Пусть направление перемещения суммирующего узла совпадает с направлением ветвления (рисунок 1.8.5, а). Тогда перемещение суммирующего узла за узел разветвления изменит сигнал в узле разветвления и, следова­тельно, изменит сигнал во всех остальных ветвях, отходящих от узла. Для того чтобы скомпенсировать это изменение, необходи­мо в отходящей ветви добавить такой же суммирующий узел, как и перемещаемый узел (рисунок 1.8.5, б).

Условие эквивалентности схем, показанных на рисунке 1.8.5 (а) и (б), определяется уравнением

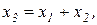(1.8.17)

справедливым для обеих схем.

Таким образом, можно сформулировать первое правило пре­образования. При перемещении суммирующего узла через узел разветвления по направлению ветвления необходимо в отходя­щих от разветвления ветвях добавить такие же, как и переме­щаемый узел, суммирующие узлы (рисунок 1.8.5, а и б).

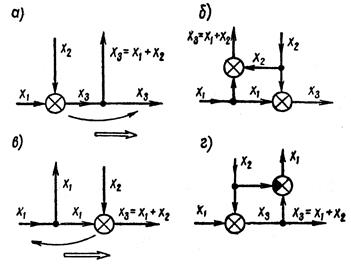
Рисунок 1.8.5 – Перемещение суммирующего узла через узел разветвления

Если направление перемещения суммирующего узла проти­воположно направлению ветвления (рисунок 1.8.5, в), то условия преобразования несколько изменяются. В этом случае для ком­пенсации влияния переноса узла необходимо не добавлять к от­ветвляемым величинам слагаемые в узле, а вычитать их (рисунок 1.8.5, г).

При этом для эквивалентности схем (в) и (г) и сохранения значений величин, подводимых к схеме и отводимых от нее, необходимо, чтобы от величины, отводимой от узла разветвле­ния, отнималась такая же величина (x₂), как и та, которая бы­ла добавлена в перенесенном суммирующем узле.

Второе правило преобразования (для этого случая) форму­лируется следующим образом. При перемещении суммирующего узла через узел разветвления против направления ветвления не­обходимо в отходящих от разветвления ветвях добавить суммирующие узлы, отличающиеся от перемещаемого знаками прибавляемых величин (рисунок 1.8.5, в и г).

Перемещение звена через узел. При переме­щении звена через узел также определяющее значение имеет направление ветвления. Рассмотрим перемещение звена по на­правлению ветвления. Если перемещение звена W₁ произво­дится через узел разветвления величины y₁ (рисунок 1.8.6, а), то условием сохранения значений величин, отводимых от схемы, является выполнение условия

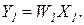(1.8.18)

Очевидно, что для соблюдения этого условия необходимо во всех отходящих от узла ветвях добавить звено с передаточной функцией W₁. Из рассмотрения схем (а) и (б), показанных на рисунке 1.8.6, видно, что они эквивалентны по отношению к внешним соединениям.

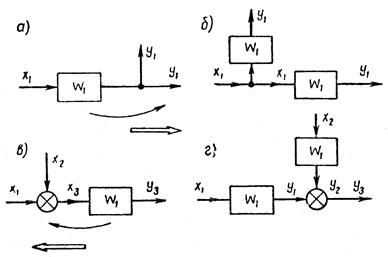
Рисунок 1.8.6 – Перемещение звена через узел по направлению ветвления

Если перемещение звена производится через суммирующий узел по направлению ветвления, то можно прийти к аналогич­ным выводам. В этом случае уравнение

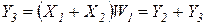(1.8.19)

выполняется, если во всех ветвях, отходящих от узла, добав­ляются звенья с передаточной функцией W₁. Условие эквива­лентности таких схем иллюстрируется схемами (в) и (г), пока­занными на рисунке 1.8.6.

Третье правило преобразования формулируется так. При пе­ремещении звена через узел по направлению ветвления необ­ходимо в подсоединенные к узлу ветви добавить звенья с пе­редаточной функцией перемещаемого звена (рисунок 1.8.6).

Если направление перемещения звена противоположно на­правлению ветвления, то условия преобразования изменяются. В этом случае для компенсации влияния звена, перенесенного в общую ветвь (на сигналы в отходящих от узла ветвях), необ­ходимо в эти ветви включить звенья с обратными передаточны­ми функциями.

Условие эквивалентности вытекает из уравнения (1.8.18) для перемещения звена через узел разветвления (рисунок 1.8.7, а и б) и из уравнения (1.8.19) для перемещения звена через сум­мирующий узел (рисунок 1.8.7, в и г).

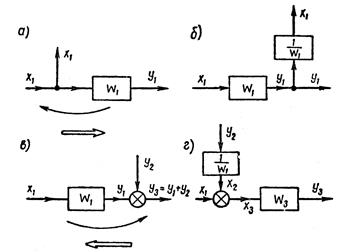
Рисунок 1.8.7 – Перемещение звена через узел против направления ветвления

Четвертое правило преобразования может быть сформули­ровано так. При перемещении звена через узел против направ­ления ветвления необходимо в подсоединенные к узлу ветви добавить звенья с передаточной функцией, обратной передаточ­ной функции перемещаемого звена (см. рисунок 1.8.7).

Применение четырех приведенных правил дает возможность производить самые различные преобразования структурных схем. При этом следует иметь в виду, что перемещение звена или узла из одной ветви в другую может производиться только при согласных направлениях передачи сигнала в этих ветвях.

Раздел 2. Исследование устойчивости линейных систем
автоматического управления. Качество процессов управления