ГЛАВА 8 РЯДЫ ФУРЬЕ И ПРЕОБРАЗОВАНИЕ ФУРЬЕ
Определение Внешней мерой Лебега множества  называется точная нижняя грань
называется точная нижняя грань 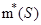 сумм длин конечного или счетного множества интервалов, покрывающих
сумм длин конечного или счетного множества интервалов, покрывающих  .
.
ЗАМЕЧАНИЕ Внешняя мера открытого множества  совпадает с его длиной, так как точная нижняя грань
совпадает с его длиной, так как точная нижняя грань 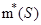 достигается на самом
достигается на самом  . Аналогичное утверждение верно для замкнутых множеств.
. Аналогичное утверждение верно для замкнутых множеств.
Определение Внутренней мерой Лебега множества 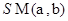 называется число
называется число 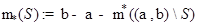 .
.
ЗАМЕЧАНИЕ Каждое ограниченное множество  имеет конечные внешнюю и внутреннюю меры, причем
имеет конечные внешнюю и внутреннюю меры, причем  .
.
Определение 1 Ограниченное множество  называется измеримым (по Лебегу), если
называется измеримым (по Лебегу), если  . В этом случае мерой Лебега множества
. В этом случае мерой Лебега множества  называется число
называется число 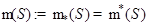 .
.
Естественным расширением класса измеримых замкнутых и открытых множеств является следующее
Определение Множество  называется борелевским, если оно представимо в виде конечного или счетного объединения или пересечения интервалов или отрезков (в любом порядке).
называется борелевским, если оно представимо в виде конечного или счетного объединения или пересечения интервалов или отрезков (в любом порядке).
ЗАМЕЧАНИЕ (свойства измеримых множеств)
1) (  -аддитивность семейства множеств) Семейство измеримых множеств замкнуто относительно операций взятия конечных и счетных объединений и пересечений.
-аддитивность семейства множеств) Семейство измеримых множеств замкнуто относительно операций взятия конечных и счетных объединений и пересечений.
2) (  -аддитивность меры) Если множества
-аддитивность меры) Если множества 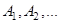 измеримы и попарно не пересекаются, то
измеримы и попарно не пересекаются, то  .
.
3) Всякое измеримое множество представимо в виде объединения борелевского множества и множества меры 0, не каждое измеримое множество будет борелевским.
4) Если  измеримо, а
измеримо, а  , то множества
, то множества  измеримы и
измеримы и  .
.
Определение 2 Множество  называется измеримым если
называется измеримым если  измеримо и
измеримо и  .
.
Определение Говорят, что какое-то свойство выполняется почти всюду на множестве, если оно выполняется во всех его точках за исключением подмножества точек меры 0.
_____
Определение Функция 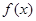 на отрезке
на отрезке  , называется измеримой, если она конечно почти всюду на
, называется измеримой, если она конечно почти всюду на  и
и 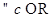 измеримо множество
измеримо множество  .
.
ЗАМЕЧАНИЕ (свойства измеримых функций)
1) Если функция 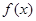 измерима, то измерима и функция
измерима, то измерима и функция 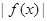 . Обратное, вообще говоря, неверно, как показывает пример функции
. Обратное, вообще говоря, неверно, как показывает пример функции 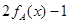 .
.
2) Если функции  измеримы, то измеримы функции
измеримы, то измеримы функции  ,
,  , причем в последнем случае предполагается, что
, причем в последнем случае предполагается, что 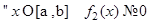 .
.
3) Пусть последовательность измеримых на  функций
функций 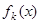 сходится почти всюду к почти всюду конечной на
сходится почти всюду к почти всюду конечной на  функции
функции 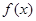 . Тогда
. Тогда 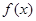 измерима на
измерима на  и
и  найдется измеримое подмножество
найдется измеримое подмножество 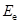 с мерой
с мерой  , на котором
, на котором 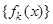 сходится к
сходится к 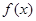 равномерно (теорема Егорова).
равномерно (теорема Егорова).
4) Если последовательность измеримых на  функций
функций 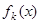 сходится почти всюду к почти всюду конечной на
сходится почти всюду к почти всюду конечной на  функции
функции 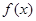 , то она сходится к
, то она сходится к 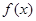 по мере:
по мере:  .
.
Обратное, вообще говоря, не верно. Однако, если последовательность измеримых функций 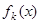 сходится к
сходится к 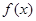 по мере, то
по мере, то  подпоследователь ность
подпоследователь ность  сходится к
сходится к 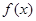 почти всюду на
почти всюду на  (теорема Рисса).
(теорема Рисса).
5) Измеримая функция совпадает почти всюду с пределом последовательности многочленов (Фреше).
_____
Определение 1 Пусть 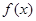 измерима и ограничена на
измерима и ограничена на  ,
,  ,
,  . Разобьем отрезок
. Разобьем отрезок 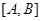 точками
точками 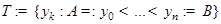 ,
,
и обозначим измеримые множества 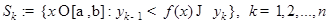 .
.
Выберем произвольно точки 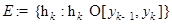 , и образуем интегральную сумму
, и образуем интегральную сумму  . Тогда предел ( можно показать, что он существует)
. Тогда предел ( можно показать, что он существует) 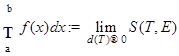 называется интегралом Лебега функции
называется интегралом Лебега функции 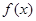 , а сама функция – суммируемой (интегрируемой по Лебегу) на отрезке
, а сама функция – суммируемой (интегрируемой по Лебегу) на отрезке  .
.
Определение 2 Пусть теперь 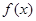 измерима и не ограничена на
измерима и не ограничена на  . Определим ограниченные измеримые функции
. Определим ограниченные измеримые функции
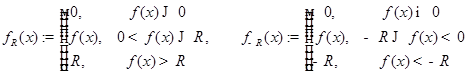 .
.
Интегралом Лебега функции 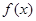 на
на  называется величина
называется величина
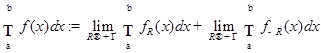 ,
,
если последние пределы существуют и конечны. При этом 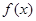 суммируемой (интегрируемой по Лебегу) на отрезке
суммируемой (интегрируемой по Лебегу) на отрезке  .
.
ЗАМЕЧАНИЕ При таком определении не всякая измеримая функция будет суммируемой, а только такая, для которой существуют и конечны пределы 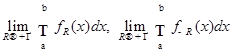 .
.
Определение 3 Пусть теперь 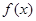 определена на
определена на 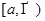 и суммируема на каждом
и суммируема на каждом  . Положим
. Положим
 .
.
Если существуют и конечны пределы  , то
, то
величина
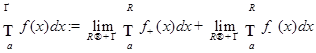
называется интегралом Лебега функции 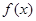 на
на 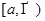 .
.
ЗАМЕЧАНИЕ 1 Аналогично определяется 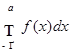 , а интеграл
, а интеграл
 ,
,
если слагаемые интегралы существуют и конечны.
ЗАМЕЧАНИЕ 2 Интеграл Лебега определяется так же на измеримом множестве 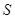 . В этом случае он обозначается
. В этом случае он обозначается 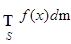 .
.
ЗАМЕЧАНИЕ 3 Аналогично определяются измеримые множества и функции в 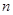 -мерном евклидовом пространстве и кратные интегралы Лебега.
-мерном евклидовом пространстве и кратные интегралы Лебега.
ЗАМЕЧАНИЕ 4 (свойства интеграла Лебега)
1) Измеримая функция  суммируема тогда и только тогда, когда суммируема
суммируема тогда и только тогда, когда суммируема  .
.
2) Если  интегрируема по Риману на
интегрируема по Риману на  , то она измерима, интегрируема по Лебегу и эти интегралы равны.
, то она измерима, интегрируема по Лебегу и эти интегралы равны.  интегрируема по Риману на
интегрируема по Риману на  тогда и только тогда, когда она ограничена на
тогда и только тогда, когда она ограничена на  и непрерывна почти всюду на нем (Лебег).
и непрерывна почти всюду на нем (Лебег).
3) Если функции  суммируемы и совпадают почти всюду на измеримом множестве
суммируемы и совпадают почти всюду на измеримом множестве 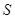 (-эквивалентные функции), то
(-эквивалентные функции), то 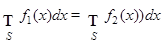 .
.
4)  для любых суммируемых функций
для любых суммируемых функций  на измеримом множестве
на измеримом множестве 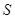
 .
.
5) Если функции  суммируемы и
суммируемы и  , то
, то 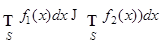 .
.
6) Для измеримого множества 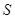
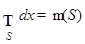 .
.
7) Пусть  , множества
, множества  измеримы и
измеримы и
функция  суммируема на
суммируема на 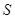 . Тогда
. Тогда  .
.
8) (теорема Лебега) Если последовательность измеримых на измеримом множестве 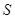 функций
функций 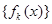 сходится по мере к
сходится по мере к  ,
, 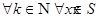
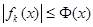 , где
, где  суммируема на
суммируема на 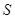 , то функции
, то функции 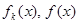 суммируемы и
суммируемы и
 .
.
____
Определение Определенная на  функция
функция  называется абсолютно непрерывной, если
называется абсолютно непрерывной, если 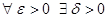 и любой системы попарно непересекающихся интервалов
и любой системы попарно непересекающихся интервалов  со свойством
со свойством 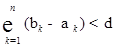 имеет место неравенство
имеет место неравенство  .
.
ЗАМЕЧАНИЕ (свойства абсолютно непрерывных функций)
1) Абсолютно непрерывная функция непрерывна на  . Обратное, вообще говоря, неверно.
. Обратное, вообще говоря, неверно.
2) Если  удовлетворяет условию Липшица на отрезке
удовлетворяет условию Липшица на отрезке  , то она абсолютно непрерывна на нем.
, то она абсолютно непрерывна на нем.
3) Если функции 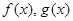 абсолютно непрерывны, то абсолютно непрерывны функции
абсолютно непрерывны, то абсолютно непрерывны функции  (в последнем случае функция
(в последнем случае функция  не должна иметь нулей на
не должна иметь нулей на  ).
).
4) Абсолютно непрерывная функция  имеет производную почти всюду на
имеет производную почти всюду на  , причем
, причем 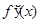 суммируема. Обратно, интеграл с переменным верхним пределом
суммируема. Обратно, интеграл с переменным верхним пределом  от суммируемой функции есть функция абсолютно непрерывная, причем
от суммируемой функции есть функция абсолютно непрерывная, причем 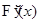 почти всюду совпадает с
почти всюду совпадает с  .
.
5) (геометрический смысл) Непрерывная на  функция
функция  будет абсолютно непрерывной тогда и только тогда, когда кривая
будет абсолютно непрерывной тогда и только тогда, когда кривая  спрямляема и
спрямляема и 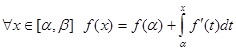 , где интеграл понимается в смысле Лебега.
, где интеграл понимается в смысле Лебега.
_____
Определение Измеримая на измеримом множестве 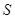 функция
функция  называется суммируемой со степенью
называется суммируемой со степенью 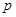 (
( 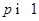 ), если функция
), если функция 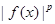 суммируема на
суммируема на 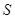 .
.
ЗАМЕЧАНИЕ (свойство суммируемых со степенью 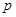 функций) 1)
функций) 1) 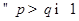 суммируемая со степенью
суммируемая со степенью 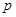 будет суммируемой со степенью
будет суммируемой со степенью  .
.
2) Для любых суммируемых со степенью 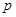 функций
функций 
 функция
функция  тоже суммируема со степенью
тоже суммируема со степенью 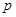 .
.
3) (неравенство Минковского) Для любых суммируемых со степенью 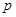 функций
функций 
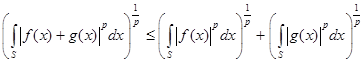 .
.
4) (неравенство Гельдера)  ,
,
если  суммируема со степенью
суммируема со степенью 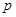 , а
, а 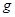 - со степенью
- со степенью  .
.
Обозначение Разобьем множество всех суммируемых со степе нью 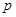 на
на  функций на классы эквивалентных функций. Интегралы представителей одного класса совпадают, и согласно замечанию множество
функций на классы эквивалентных функций. Интегралы представителей одного класса совпадают, и согласно замечанию множество 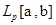 этих классов удовлетворяет аксиомам векторного пространства.
этих классов удовлетворяет аксиомам векторного пространства.
Определение 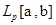 -пространство суммируемых со степенью
-пространство суммируемых со степенью 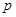 функций.
функций. 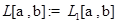 - пространство суммируемых функций.
- пространство суммируемых функций.
ЗАМЕЧАНИЕ (свойства пространства 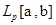 )
)
1) Величина  является нормой в
является нормой в 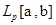 , а нормированное пространство
, а нормированное пространство 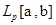 является полным и значит банаховым.
является полным и значит банаховым.
2) Если последовательность  сходится в среднем со степенью
сходится в среднем со степенью 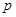 к
к  , то есть
, то есть  , то она сходится к
, то она сходится к  по мере. Обратное, вообще говоря, не верно.
по мере. Обратное, вообще говоря, не верно.
3)  является гильбертовым пространством относительно скалярного произведения
является гильбертовым пространством относительно скалярного произведения 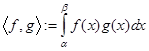 , то есть оно является банаховым пространством относительно нормы
, то есть оно является банаховым пространством относительно нормы 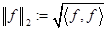 .
.
4) Множество многочленов всюду плотно в 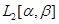 :
:
 .
.
_____
Определение Комплексным евклидовым пространством называется пара 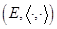 , состоящая из векторного пространства
, состоящая из векторного пространства 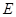 над полем
над полем 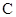 комплексных чисел, и билинейной формы
комплексных чисел, и билинейной формы 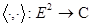 со свойствами: 1)
со свойствами: 1) 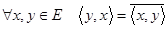 , 2)
, 2) 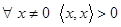 .
.
ЗАМЕЧАНИЕ Скалярное произведение определяет на 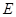 норму
норму 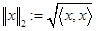 .
.
Определение Последовательность элементов 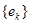 называется ортонормирован ной, если ее элементы попарно ортогональны:
называется ортонормирован ной, если ее элементы попарно ортогональны: 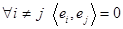 , и нормированным:
, и нормированным: 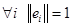 , то есть
, то есть 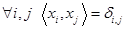 .
.
Определение Пусть 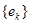 -ортонормированная последовательность в евклидовом пространстве
-ортонормированная последовательность в евклидовом пространстве 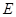 . Числа
. Числа  , называются коэффициентами Фурье элемента
, называются коэффициентами Фурье элемента  по системе
по системе 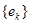 .
.
Определение Сумма 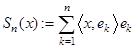 называется
называется  -ой частичной суммой, а ряд
-ой частичной суммой, а ряд 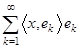 - рядом Фурье элемента
- рядом Фурье элемента  .
.
Определение Член 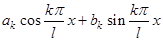 называется
называется  -ой гармоникой тригонометрического ряда
-ой гармоникой тригонометрического ряда 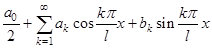 .
.
Если положить  и определить угол
и определить угол  из системы
из системы 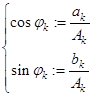 , то
, то  -ю гармонику можно записать в виде
-ю гармонику можно записать в виде 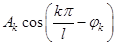 .
.
Определение Пусть
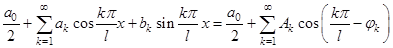
есть тригонометрический ряд Фурье  -периодической функции
-периодической функции  . Последовательность
. Последовательность 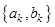 или
или  называется спектром периодической функции
называется спектром периодической функции  ;
;  - амплитудой
- амплитудой  -ой гармоники;
-ой гармоники; 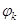 - фазой
- фазой  -ой гармоники.
-ой гармоники.  - основная частота;
- основная частота; 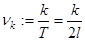 -
-  -ая гармоническая частота.
-ая гармоническая частота.  - основная круговая частота;
- основная круговая частота;  -
-  -ая круговая частота функции
-ая круговая частота функции  .
.
ТЕОРЕМА 8.1 (свойства сходимости ряда Фурье по норме)
1) Пусть  ортонормированная последовательность в вещественном евклидо вом пространстве
ортонормированная последовательность в вещественном евклидо вом пространстве 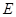 . Для каждого элемента
. Для каждого элемента  существует единственный "многочлен"
существует единственный "многочлен"  степени
степени  , отклонение которого от элемента
, отклонение которого от элемента  будет наименьшим:
будет наименьшим:  .
.
2) Для каждого элемента  гильбертова пространства
гильбертова пространства 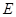 его ряд Фурье сходится по норме
его ряд Фурье сходится по норме 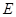 . Для того, чтобы он сходился к самому элементу, необходимо и достаточно, чтобы имело место равенство Парсеваля
. Для того, чтобы он сходился к самому элементу, необходимо и достаточно, чтобы имело место равенство Парсеваля 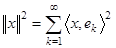 .
.
3) Для каждой функции 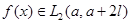 ее тригонометрический ряд
ее тригонометрический ряд
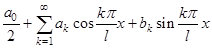 сходится к
сходится к  по норме.
по норме.
СЛЕДСТВИЕ Для каждой функции 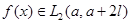 равенство
равенство
Парсеваля принимает вид  .
.
Определение Пусть  суммируема на некоторой окрестности точки
суммируема на некоторой окрестности точки 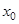 . Говорят, что
. Говорят, что  удовлетворяет условию Дини в этой точке, если
удовлетворяет условию Дини в этой точке, если 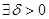 существует интеграл в смысле Лебега
существует интеграл в смысле Лебега
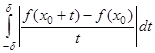 .
.
ЗАМЕЧАНИЕ Дифференцируемая в точке 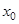 функция удовлетворяет условию Дини, а непрерывная в этой точке - вообще говоря, нет.
функция удовлетворяет условию Дини, а непрерывная в этой точке - вообще говоря, нет.
ТЕОРЕМА 8.2 (свойства поточечной сходимости тригонометрического ряда Фурье)
1) Если  суммируема на отрезке
суммируема на отрезке  и удовлетворяет условию Дини в точке
и удовлетворяет условию Дини в точке  , то ее тригонометрический ряд Фурье сходится в этой точке к
, то ее тригонометрический ряд Фурье сходится в этой точке к  . Существует суммируемая функция, ряд Фурье которой сходится всюду на
. Существует суммируемая функция, ряд Фурье которой сходится всюду на  (Колмогоров).
(Колмогоров).
2) (Лузин-Карлесон) Для каждой функции 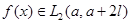 ее тригонометри ческий ряд сходится к
ее тригонометри ческий ряд сходится к  почти всюду на
почти всюду на  .
.
3) Пусть функция 
 -периодическая на всей оси, имеет разрывы только первого рода и имеет правые и левые производные в каждой точке. Тогда ее тригонометрический ряд Фуре в каждой точке
-периодическая на всей оси, имеет разрывы только первого рода и имеет правые и левые производные в каждой точке. Тогда ее тригонометрический ряд Фуре в каждой точке  сходится к числу
сходится к числу  .
.
4) В условиях предыдущего пункта  представима в этом же смысле в виде ряда Фурье в комплексной форме
представима в этом же смысле в виде ряда Фурье в комплексной форме 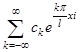 , причем
, причем  и коэффициенты
и коэффициенты 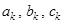 связаны равенством
связаны равенством  .
. 
5) Если функция  четная (нечетная) на
четная (нечетная) на 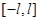 и удовлетворяет условиям пункта 4), то
и удовлетворяет условиям пункта 4), то 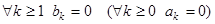 , то есть она разлагается в ряд по косинусам (по синусам) на оси. При этом
, то есть она разлагается в ряд по косинусам (по синусам) на оси. При этом
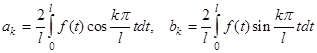 .
.
6) Пусть функция 
 -периодическая и непрерывная на всей оси. Тогда
-периодическая и непрерывная на всей оси. Тогда 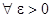 существует тригонометрический многочлен
существует тригонометрический многочлен  со свойством
со свойством 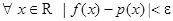 (Вейерштрасс). Существует непрерывная на
(Вейерштрасс). Существует непрерывная на  функция, тригонометрический ряд Фурье которой расходится во всех точках из
функция, тригонометрический ряд Фурье которой расходится во всех точках из 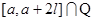 (Колмогоров).
(Колмогоров).
7) Если функция  абсолютно непрерывна на
абсолютно непрерывна на  ,
,  , то ее тригонометрический ряд Фурье сходится к
, то ее тригонометрический ряд Фурье сходится к  равномерно на всей оси.
равномерно на всей оси.
_____
Определение Пусть 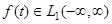 . Можно показать, что интеграл
. Можно показать, что интеграл 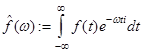 ,
, 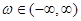 , сходится. Он называется преобразованием Фурье функции
, сходится. Он называется преобразованием Фурье функции 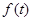 .
.
ЗАМЕЧАНИЕ 1) (физический смысл) Если 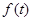 рассматривается как аналоговый сигнал (например, электрический) и
рассматривается как аналоговый сигнал (например, электрический) и 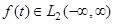 , то преобразование Фурье
, то преобразование Фурье 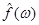 называется непрерывным (интегральным) спектром этого сигнала, а его энергия пропорциональна норме
называется непрерывным (интегральным) спектром этого сигнала, а его энергия пропорциональна норме 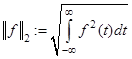 . При этом область опреде ления сигнала
. При этом область опреде ления сигнала 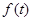 называется временной областью, а область определения спектра
называется временной областью, а область определения спектра 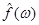 - частотной областью.
- частотной областью.
2) Пусть выполнено одно из условий:
а) 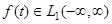 и удовлетворяет условию Дини в точке
и удовлетворяет условию Дини в точке  ;
;
б) 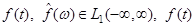 непрерывна в точке
непрерывна в точке  .
.
Тогда имеет место формула обращения в этой точке  .
.
ТЕОРЕМА 8.3 (свойства преобразования Фурье)
1) Преобразование Фурье является линейным отображением.
2) Если 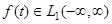 , то
, то 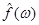 ограничена, непрерывна на
ограничена, непрерывна на  , и
, и
 .
.
3) Если 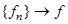 по норме пространства
по норме пространства 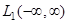 , то
, то 
равномерно на  .
.
4) Если 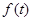
 раз дифференцируема на
раз дифференцируема на  и
и  , то
, то
 .
.
5) Если 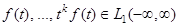 , то
, то 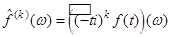 .
.
6) Если 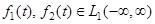 , то существует их свертка
, то существует их свертка
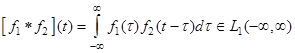 и
и 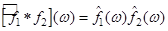 .
.
ЗАМЕЧАНИЕ 1 Если 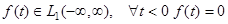 , то
, то
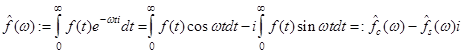 ,
,
где отображение 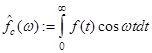 называется косинус-преобразо
называется косинус-преобразо
ванием, а  - синус-преобразованием функции
- синус-преобразованием функции
 .
.
Дата добавления: 2015-08-26; просмотров: 1427;
