ГЛАВА 9 УРАВНЕНИЯ В ЧАСТНЫХ ПРОИЗВОДНЫХ

Определение Дифференциальное уравнение вида

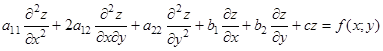, (1)

где 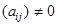, 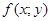- известная функция в области 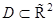, 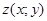- искомое реше ние области 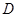, называется линейным дифференциальным уравнением в част ных производных (ЛДУЧП) второго порядка с постоянными коэффициентами .

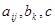Определение ЛДУЧП называется:

уравнением эллиптического типа, если ,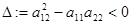

уравнением параболического типа, если ,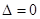

уравнением гиперболического типа, если .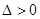

ЗАМЕЧАНИЕ С помощью подходящей замены переменных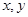

и зависимой переменной 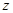, ЛДУЧП можно привести к виду:

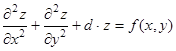- канонический вид ЛДУЧП эллиптического типа,

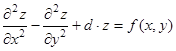- канонический вид ЛДУЧП гиперболического типа

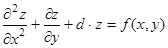- канонический вид ЛДУЧП параболического

типа.

ЗАМЕЧАНИЕ Уравнение эллиптического типа

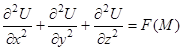
описывает пространственные стационарные процессы: упругие

деформации, электростатические поля и другие.

ЗАМЕЧАНИЕ 1 В случае 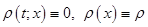уравнение

,

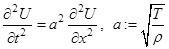называют уравнение свободных колебаний струны.

ЗАМЕЧАНИЕ 2 Уравнение свободных колебаний мембраны

(свободно изгибающейся натянутой пленки 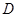в плоскости )

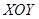имеет вид

,

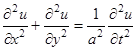где 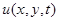- аппликата точки 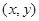мембраны в момент времени t.

ЗАМЕЧАНИЕ Аналогично выводится уравнение теплопровод

ности однородного тела

.

_____

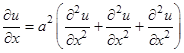Определение Пусть на границе 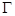области 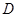(или на её части) заданы функции 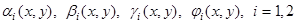. Система уравнений вида

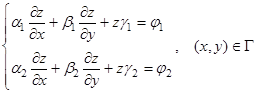, (2)

называется граничными условиями. Задача нахождение решения 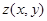ЛДУЧП (1) в области 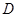, предельные значения которого удовлетворяют граничным условиям, называется граничной задачей.

Определение Граничная задача с условием 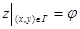, называется задачей Дирихле.

Определение Граничная задача с условием

,

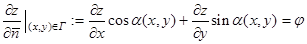где 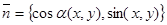- вектор внутренней нормали в точке , называется задачей Неймана.

Определение Если на разных участках границы искомое решение удовлетворяет разным по форме условиям, то, соответствующая граничная задача называется смешанной.

Определение Если одна из переменных является по смыслу временем 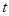и часть границы задается уравнением 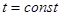, то граничная задача называется задачей Коши с соответствующим начальным условием. Остальные условия при этом нередко называют краевыми.

Вопросы к первому блоку, 2010-2011 уч. год

1. Опр. ДУ, ОДУ. Пр. 2. Опр. ОДУ 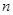-го порядка, разрешенного (неразрешенно го) относительно производной. 3. Опр. решения ОДУ и интегральной кривой. Пр 4. Опр. задачи Коши, условий и данных Коши. 5. Опр. общего, частного и особого решений. 6. Что значит проинтегрировать в явном виде и в квадрату рах? Пр. 7. Опр. НСОДУ, его порядка и задачи Коши. 8. Опр. НСЛДУ, однородной НСЛДУ и линейно независимых решений. 9. Опр. фундаменталь ной системы решений, фундамент. матрицы и вронскиана. 10. Опр. переходной матрицы и ее свойства. 11. Опр. ЛДУ 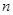-го порядка и его свойства. 12. Опр. подобных матриц, матрицы перехода и характеристического многочлена матрицы. 13. Опр. собственного числа, соб. вектора, и 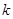-го присоединенного вектора. 14. Опр. показателя нильпотентности и корневого подпространства. 16. Опр. суммы и прямой суммы подпространств. Замеч. 17. Опр. матричного и аннулирующего многочлена. Замеч. 18. Опр. жордановой клетки и теорема Кели-Гамильтона. 19. Опр. операции овеществления ЖНФ. Замеч. 20. Опр. метода расщепления. 21. Опр. задачи простой интерполяции и формула Лагранжа. 22. Опр. задачи кратной интерполяции и формулы Эрмита. 23. Опр. сплайна, естественного и периодического сплайнов. 24. Алгоритм построения кубического сплайна. 25. Опр. аннулирующего и минимального аннулирующее го многочлена. 26.Опр. нормированного, полного и гильбертова пространств. Пр. 27. Опр. спектра матрицы, функций, совпадающих на спектре.

Вопросы ко второму блоку, 2010-2011 уч.год

1) Опр. сетки и сеточной функции. 2) Опр. локальной, глобальной погрешнос тей и метод Эйлера. 3) Опр. автономной системы и положения равновесия. Зам. 4) Опр. фазовых траектории, пространства и портрета. Зам. 5) Опр. замкнутого и предельного циклов. Зам. 6) Опр. предельного, притягивающего и отталкивающе го циклов. 7) Опр. устойчивого и неустойчивого узлов. Рис. 8) Опр. устойчивого и неустойчивого фокусов. Рис. 9) Опр. седла и центра. Рис. 10) Опр. устойчивости по Ляпунову и асимптотической устойчивости. Зам. 11) Опр. линеаризации НСОДУ. 12) Опр-е интеграла Лебега. 13) Свойства интеграла Лебега. 14) Опр. пространства 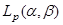. Св. 15) Опр.комплексного евклидова про-ва, ортонормированной системы и коэффициентов Фурье. Пр. 16) Опр. ряда Фурье и условия. Дини. Пр. 17) Опр. к-ой гармоники, спектра периодической функции, амплитуд, фазы, частот. 18) Опр. преобразования Фурье, спектра. Физ. смысл. 19) Опр. 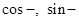преобразования, и связь с преобразо ванием Лапласа. 20) Опр. обобщ. преобразования Фурье. Пр. 21) Опр. ЛДУЧП второго порядка и канонический вид 22) Опр. граничной задачи, задач Дирихле, Неймана и Коши.