ГЛАВА 7 ОБЫКНОВЕННЫЕ ДИФФЕРЕНЦИАЛЬНЫЕ УРАВНЕНИЯ
Определение Дифференциальным уравнением называется уравнение, содержащее неизвестную функцию, независимые переменные и производные этой функции.
Определение Дифференциальное уравнением, в котором независимых переменных более одной, называется дифференциальным уравнением в частных производных (ДУЧП ).
Определение Дифференциальное уравнением, в котором независимая переменная одна, называется обыкновенным дифференциальным уравнением (ОДУ).
Определение Дифференциальным уравнением n-ого порядка
называется ОДУ, в котором самый высокий порядок производной неизвестной функции равен 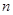 .
.
Определение ОДУ вида  называется уравнением, разрешенным относительно старшей производной
называется уравнением, разрешенным относительно старшей производной 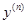 . ОДУ вида
. ОДУ вида 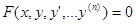 называется уравнением общего вида. Здесь
называется уравнением общего вида. Здесь 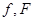 - известные функции.
- известные функции.
В терминах дифференциальных уравнений формулируются законы, по которым развиваются или связываются между собой процессы.
Определение Решением ОДУ 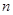 -ого порядка на интервале
-ого порядка на интервале 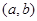
называется 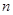 раз дифференцируемая на
раз дифференцируемая на 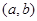 функция, которая при
функция, которая при
подстановке в уравнение обращает его в тождественное равенство на 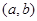 .
.
Определение График решения ОДУ называется интегральной кривой.
Определение Пусть дано ОДУ 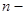 ого порядка и числа
ого порядка и числа 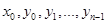 . Задача нахождения решения ОДУ в окрестности точки
. Задача нахождения решения ОДУ в окрестности точки 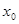 , которое удовлетворяет равенствам
, которое удовлетворяет равенствам 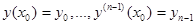 , называется задачей Коши. Сами равенства называются условиями Коши, а числа
, называется задачей Коши. Сами равенства называются условиями Коши, а числа 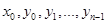 - данными Коши.
- данными Коши.
Определение Общим решением ОДУ n- ого порядка в окрестности точки 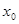 называется функция
называется функция 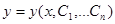 , зависящая от
, зависящая от 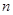 параметров
параметров 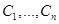 , которая при подстановке в уравнение обращает его в тождество.
, которая при подстановке в уравнение обращает его в тождество.
Определение Решение, получаемое из общего при конкретных значениях параметров, называется частным.
Определение Решение ОДУ , в каждой точке которого нарушается единственность решения задачи Коши, называется особым.
Определение Решение, заданное в виде неявной функции 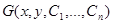 и зависящее от
и зависящее от 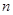 произвольных параметров, называется общим интегралом.
произвольных параметров, называется общим интегралом.
Определение Проинтегрировать ОДУ в явном виде – это значит найти
его общее решение в виде элементарной функции.
Определение Проинтегрировать ОДУ в квадратурах – это значит найти его общее решение в виде интегралов от элементарных функций. и второго порядков
_____
Определение ОДУ вида 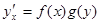 или вида
или вида 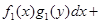
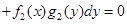 называется ОДУ с разделяющимися переменными.
называется ОДУ с разделяющимися переменными.
Определение ОДУ вида 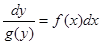 или вида
или вида 
 называется ОДУ с разделенными переменными.
называется ОДУ с разделенными переменными.
ЗАМЕЧАНИЕ Решения этих уравнений выписываются в
квадратурах: 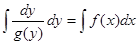 ,
, 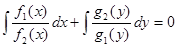 .
.
_____
Определение Функция 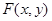 называется однородной функцией степени
называется однородной функцией степени 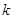 , если
, если 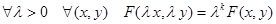 .
.
Определение ОДУ вида 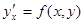 или вида
или вида 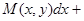
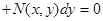 называется однородным, если соответственно
называется однородным, если соответственно 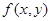 - однородная функция нулевой степени,
- однородная функция нулевой степени, 
 - однородные
- однородные
функции одинаковой степени.
ЗАМЕЧАНИЕ Однородное ОДУ преобразуется в ОДУ с
разделяющимися переменными, если зависимую переменную 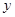
заменить на 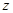 по формуле
по формуле 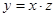 .
.
_____
Определение Дифференциальное уравнение вида 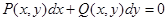 называется ОДУ в полных дифференциалах, если функции
называется ОДУ в полных дифференциалах, если функции 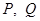 имеют непрерывные частные производные и
имеют непрерывные частные производные и  .
.
ЗАМЕЧАНИЕ ОДУ в полных дифференциалах решается в
квадратурах. Последнее условие равносильно существованию функции
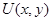 с дифференциалом
с дифференциалом 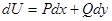 . Тогда общий интеграл имеет
. Тогда общий интеграл имеет
вид 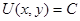 .
.
_____
Определение ОДУ вида 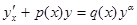 , где функции
, где функции 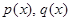 заданы и непрерывны, называется уравнением Бернулли, если
заданы и непрерывны, называется уравнением Бернулли, если 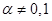 и линейным уравнением (ЛДУ) в противном случае.
и линейным уравнением (ЛДУ) в противном случае.
ЗАМЕЧАНИЕ Эти ОДУ решается методом вариации
произвольной постоянной. 1) Сначала решается ОДУ с
разделяющимися переменными 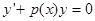 .
.
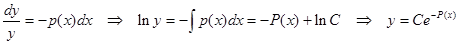 .
.
2) Решение исходного уравнения 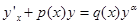 ищем в виде
ищем в виде
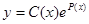 , считая в предыдущем решении произвольную
, считая в предыдущем решении произвольную
постоянную зависящей от 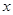 (говорят: варьируя произвольную
(говорят: варьируя произвольную
постоянную 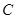 ). Для нахождения
). Для нахождения 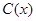 подставим это решение в
подставим это решение в
исходное уравнение: 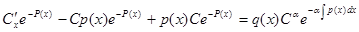 .
.
После сокращения получаем уравнение с разделяющимися
переменными для нахождения 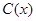 .
.
____
ЗАМЕЧАНИЕ 1 Решение ОДУ второго порядка вида 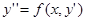
сводится к решению ОДУ первого порядка 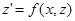 с помощью
с помощью
замены 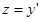 .
.
ЗАМЕЧАНИЕ 2 Решение ОДУ второго порядка вида 
сводится к решению ОДУ первого порядка с помощью замены 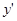
на зависимую переменную 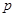 .
.
_____
Определение Нормальной системой обыкновенных дифференциальных уравнений (НСОДУ) называется система вида
 ,
,
где функции 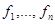 непрерывны на открытом множестве
непрерывны на открытом множестве 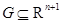 , а последовательность неизвестных функций
, а последовательность неизвестных функций 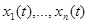 называется решением системы. Число
называется решением системы. Число 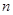 называется порядком НСОДУ.
называется порядком НСОДУ.
Определение Если 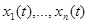 - решение НСОДУ в окрестности точки
- решение НСОДУ в окрестности точки 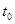 , то кривая в
, то кривая в 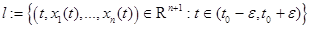 называется интегральной кривой.
называется интегральной кривой.
Определение Пусть 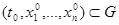 . Задачей Коши для НСОДУ с начальными условиями
. Задачей Коши для НСОДУ с начальными условиями 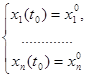 называется задача нахождения решения системы в окрестности точки
называется задача нахождения решения системы в окрестности точки 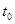 , которое удовлетворяет этим условиям.
, которое удовлетворяет этим условиям.
Пример Решение задачи Коши для ОДУ 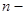 го порядка
го порядка 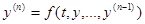 с начальными условиями
с начальными условиями 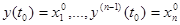 равносильно нахождению решения задачи Коши для НСОДУ
равносильно нахождению решения задачи Коши для НСОДУ
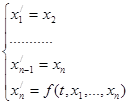
с начальными условиями 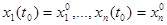 .
.
Определение Функция 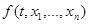 удовлетворяет условию Липшица по переменным
удовлетворяет условию Липшица по переменным 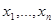 на множестве
на множестве 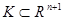 , если
, если
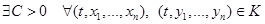
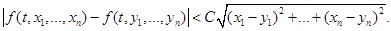
ТЕОРЕМА 7.1 Пусть функции 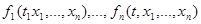
непрерывны на открытом множестве 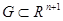 и удовлетворяют
и удовлетворяют
условию Липшица по 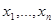 на любом замкнутом ограниченном
на любом замкнутом ограниченном
подмножестве в 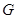 . Тогда
. Тогда 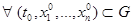 в окрестности точки
в окрестности точки 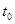
существует единственное решение 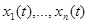 задачи Коши для
задачи Коши для
НСОДУ с начальным условием 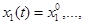
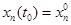 . Если
. Если
отказаться от условия Липшица, то решение задачи Коши
существует, но оно, вообще говоря, неединственное.
Определение Нормальной системой линейных дифференциальных уравнений (НСЛДУ) называется система вида
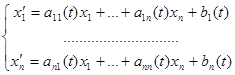
или в матричной форме 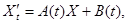 где
где 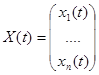 - искомое решение на
- искомое решение на 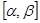 ;
; 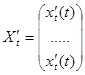 ;
; 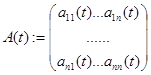 - матрица непрерывных на
- матрица непрерывных на 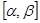 коэффициентов;
коэффициентов; 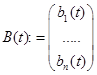 - матрица непрерывных на
- матрица непрерывных на 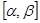 свободных членов.
свободных членов.
Определение НСЛДУ называется однородной, если 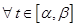
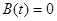 , и неоднородной в противном случае.
, и неоднородной в противном случае.
Определение Последовательность 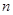 решений
решений 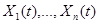 однородной НСЛДУ называется фундаментальной системой, если
однородной НСЛДУ называется фундаментальной системой, если 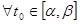 векторы
векторы 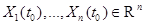 линейно независимы. Определитель и матрица
линейно независимы. Определитель и матрица
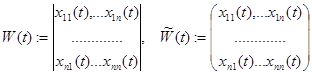
называются соответственно вронскианом и фундаментальной матрицей (матрицей Вронского) НСЛДУ.
Последняя есть пример функциональной матрицы.
Определение Производной функциональной матрицы 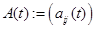
называется функциональная матрица 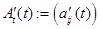 ; интегралом функциональной матрицы
; интегралом функциональной матрицы  на отрезке
на отрезке 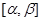 называется числовая матрица
называется числовая матрица 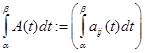 .
.
ТЕОРЕМА 7.2 (Свойства решений НСЛДУ)
1)  существует единственное решение на
существует единственное решение на
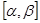 задачи Коши с начальным условием
задачи Коши с начальным условием 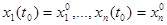 .
.
2) Систем 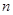 решений
решений 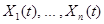 фундаментальна на отрезке
фундаментальна на отрезке 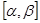
тогда и только тогда, когда 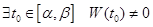 ;
;
3) Если система решений 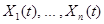 фундаментальна на
фундаментальна на 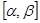 , то
, то
общее решение однородной НСЛДУ 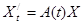 имеет вид
имеет вид
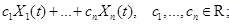 .
.
4) Если 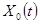 - какое-либо (частное) решение неоднородной НСЛДУ,
- какое-либо (частное) решение неоднородной НСЛДУ,
то общее (любое) решение этой НСЛДУ имеет вид
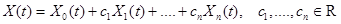 ,
,
где 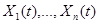 - фундаментальная система.
- фундаментальная система.
5) если известна фундаментальная система 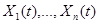 , то частное
, то частное
решение неоднородной НСЛДУ можно вычислить по формуле
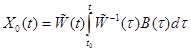 , а решение задачи Коши с начальным
, а решение задачи Коши с начальным
условием 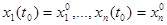 - по формуле Коши
- по формуле Коши
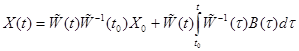 , где
, где 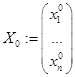 .
.
Определение Если 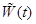 - фундаментальная матрица НСЛДУ, то матрица
- фундаментальная матрица НСЛДУ, то матрица 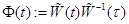 называется переходной (импульсной) матрицей этой системы.
называется переходной (импульсной) матрицей этой системы.
ЗАМЕЧАНИЕ 1) Переходная матрица является решением задачи
Коши для матричного уравнения 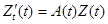 с функциональной
с функциональной
матрицей 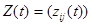 размера
размера 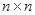 и начальным условием
и начальным условием 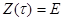 ,
,
где 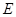 есть единичная матрица.
есть единичная матрица.
2) Переходная матрица не зависит от выбора фундаментальной системы и
полностью определяется матрицей коэффициентов 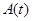 НСЛДУ.
НСЛДУ.
3) В терминах переходной матрицы формула Коши принимает вид
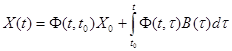 .
.
_____
Определение Линейным дифференциальным уравнением 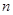 -го порядка (ЛДУ) называется ОДУ вида
-го порядка (ЛДУ) называется ОДУ вида
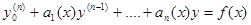 , (1)
, (1)
где функции 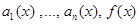 непрерывны на
непрерывны на 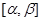 . ЛДУ называется однородным, если
. ЛДУ называется однородным, если 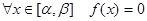 и неоднородным в противном случае.
и неоднородным в противном случае.
Определение Последовательность решений 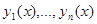 однородно ЛДУ
однородно ЛДУ 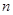 -го порядка называется линейно независимой на
-го порядка называется линейно независимой на 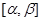 , если в каждой точке
, если в каждой точке 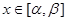 векторы
векторы 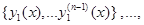
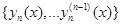 линейно независимы.
линейно независимы.
Определение Последовательность 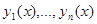 линейно независимых на
линейно независимых на 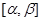 решений однородного уравнения называется фундаментальной.
решений однородного уравнения называется фундаментальной.
Определение Определителем Вронского и фундаментальной матрицей однородного ЛДУ называются соответственно
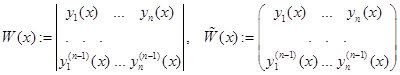 ,
,
где 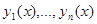 есть последовательности линейно независимых решений.
есть последовательности линейно независимых решений.
ТЕОРЕМА 7.3 (свойства решений ЛДУ 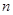 -го порядка)
-го порядка)
1) 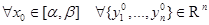 задача Коши с начальным условием
задача Коши с начальным условием
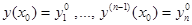 имеет единственное решение на
имеет единственное решение на 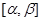 .
.
2) Решения 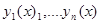 однородного ЛДУ линейно независимы на
однородного ЛДУ линейно независимы на
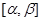 тогда и только тогда, когда
тогда и только тогда, когда 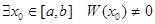 .
.
3) Если 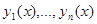 - фундаментальная последовательность
- фундаментальная последовательность
решений однородного ЛДУ, то любое (общее) его решение имеет
вид 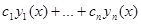
4) Если 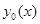 -какое-либо решение ЛДУ (1) и
-какое-либо решение ЛДУ (1) и 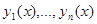 - фундамен
- фундамен
тальная последовательность решений, то любое (общее) решение
ЛДУ можно записать в виде 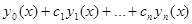 .
.
_____
Определение Матрицы 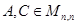 называются подобными, если существует невырожденная матрица
называются подобными, если существует невырожденная матрица  (матрица перехода от
(матрица перехода от 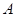 к
к 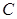 ) со свойством
) со свойством  .
.
Определение Если к множеству собственных векторов,
соответствующих собственному числу 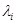 добавить нулевой вектор,
добавить нулевой вектор,
то получим подпространство  пространства в
пространства в 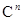 . Его
. Его
 называют подпространством собственных векторов.
называют подпространством собственных векторов.
Цель параграфа - обосновать подобные рассуждения в общем случае.
Определение Если 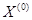 - собственный вектор, соответствующий собственному числу
- собственный вектор, соответствующий собственному числу 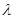 , то
, то 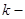 ым присоединенным вектором матрицы к
ым присоединенным вектором матрицы к 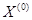 называется вектор
называется вектор 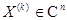 со свойством
со свойством 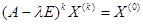 .
.
Определение Последовательность 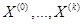 собственного и присоединенных к нему векторов называется жордановой цепочкой длины
собственного и присоединенных к нему векторов называется жордановой цепочкой длины 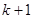 матрицы
матрицы 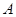 . ЗАМЕЧАНИЕ Пусть собственные векторы, образующие жордановы цепочки
. ЗАМЕЧАНИЕ Пусть собственные векторы, образующие жордановы цепочки 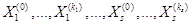 , линейно независимы и порождены одним и тем же собственным числом
, линейно независимы и порождены одним и тем же собственным числом 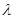 . Тогда все векторы, составляющие эти цепочки, линейно независимы.
. Тогда все векторы, составляющие эти цепочки, линейно независимы.
В силу сделанного замечания жорданова цепочка имеет длину 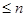 . Из импликации
. Из импликации 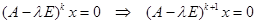 следует такая цепь вложений
следует такая цепь вложений
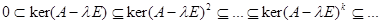 .
.
Так как каждый ненулевой вектор из 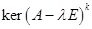 является собственным или присоединенным (высотой
является собственным или присоединенным (высотой 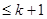 ), то есть входит в какую-то цепочку, то эти пространства, начиная с некоторого
), то есть входит в какую-то цепочку, то эти пространства, начиная с некоторого 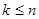 , обязаны совпадать.
, обязаны совпадать.
Определение Наименьшее число 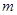 , начиная с которого все подпространства
, начиная с которого все подпространства 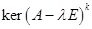 совпадают, называется показателем нильпотентности матрицы
совпадают, называется показателем нильпотентности матрицы 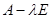 , а подпространство
, а подпространство 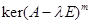 - корневым подпространством матрицы
- корневым подпространством матрицы 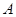 .
.
ЗАМЕЧАНИЕ Корневое подпространство является инвариант
ным относительно матричного оператора:
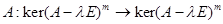 ,
,
и образовано из нуля и всех собственных и присоединенных
векторов, соответствующих собственному числу 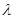 .
.
_____
Определение Система цепочек J называется жордановым базисом корневого подпространства 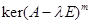 .
.
ЗАМЕЧАНИЕ По построению J 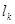 есть число жордановых
есть число жордановых
цепочек длины 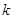 . Оно вычисляется по формуле
. Оно вычисляется по формуле
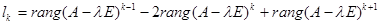 . ( 1 )
. ( 1 )
Общее число цепочек, составляющих базис J равно
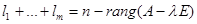 .
.
_____
Определение Суммой подпространств 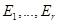 векторного пространства
векторного пространства 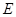 называется множество
называется множество
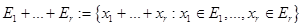 .
.
Из определения следует такое
ЗАМЕЧАНИЕ 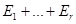 - подпространство.
- подпространство.
Определение Сумма ненулевых подпространств 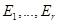 называется прямой, если
называется прямой, если  .
.
Обозначение 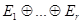 .
.
Определение Квадратную матрицу 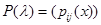 , элементами которой являются многочлены
, элементами которой являются многочлены 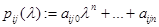 , можно представить в виде матричного многочлена
, можно представить в виде матричного многочлена 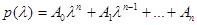 , где
, где 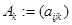 - матрица-коэффициент при
- матрица-коэффициент при 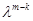 . Если
. Если 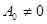 , то
, то 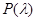 называется матричным многочленом n-ой степени.
называется матричным многочленом n-ой степени.
Определение Многочлен 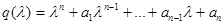 называется аннулирующим многочленом матрицы
называется аннулирующим многочленом матрицы 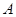 , если многочлен от матрицы
, если многочлен от матрицы 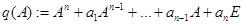 равен нулевой матрице:
равен нулевой матрице: 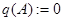 .
.
ЗАМЕЧАНИЕ (теорема Гамильтона-Кели) Характеристический
многочлен 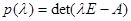 матрицы
матрицы 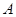 является ее аннулирующим
является ее аннулирующим
многочленом.
СЛЕДСТВИЕ Если 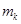 - показатель нильпотентности матрицы
- показатель нильпотентности матрицы
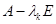 , где
, где 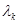 есть нуль порядка
есть нуль порядка 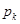 характеристического
характеристического
многочлена матрицы 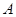 , то
, то  .
.
ТЕОРЕМА 7.4 Пусть 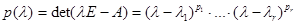 есть
есть
характеристический многочлен матрицы 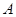 ,
, 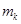 - показатель ниль
- показатель ниль
потентности матрицы 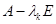 и
и 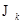 - жорданов базис корневого
- жорданов базис корневого
подпространства 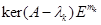 . Тогда
. Тогда
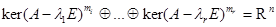 (=
(= 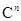 )
)
и 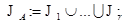 есть базис в
есть базис в 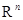 (в
(в 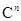 ), если все собственные
), если все собственные
числа вещественные (не все вещественные).
Определение Построенный в теореме базис 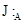 называется жордановым базисом матрицы
называется жордановым базисом матрицы 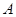 .
.
Определение Матрица 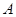 есть матрица оператора умножения на
есть матрица оператора умножения на 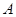 в естественном базисе пространства
в естественном базисе пространства 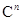 (
( 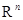 ). Найдем матрицу этого оператора в жордановом базисе. Столбцы искомой матрицы по определению составлены из коэффициентов разложения элементов вида
). Найдем матрицу этого оператора в жордановом базисе. Столбцы искомой матрицы по определению составлены из коэффициентов разложения элементов вида 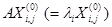 или вида
или вида 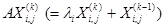 в жордановом базисе. Поэтому искомая матрица образована матрицами вида
в жордановом базисе. Поэтому искомая матрица образована матрицами вида
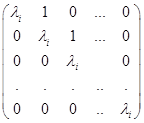 , ( 2 )
, ( 2 )
размер которых совпадает с длиной цепочки, в которую входит 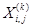 . Эти матрицы «нанизаны» на главную диагональ, а элементы вне этих матриц равны нулю. Так построенная квазидиагональная матрица называется жордановой нармальной формой (ЖНФ) матрицы
. Эти матрицы «нанизаны» на главную диагональ, а элементы вне этих матриц равны нулю. Так построенная квазидиагональная матрица называется жордановой нармальной формой (ЖНФ) матрицы 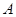 и обозначается
и обозначается 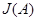 . Матрицы вида (2) называются
. Матрицы вида (2) называются 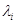 -жордановыми клетками соответствующего порядка.
-жордановыми клетками соответствующего порядка.
_____
Определение Переход от жордановой нормальной формы 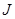 с комплексными элементами и матрицей перехода
с комплексными элементами и матрицей перехода  к вещественным матрицам
к вещественным матрицам 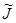 и
и 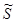 называется операцией овеществления жордановой нормальной формы.
называется операцией овеществления жордановой нормальной формы.
ЗАМЕЧАНИЕ (решение НСЛДУ с постоянными коэффициентами методом расщепления) Пусть требуется найти общее решение НСЛДУ 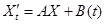 . Подставляя
. Подставляя 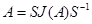 в систему и делая замену
в систему и делая замену 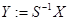 , получаем новую НСЛДУ
, получаем новую НСЛДУ 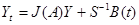 . Эта система распадается на более простые независимые НСЛДУ в количестве, равном числу клеток Жордана матрицы
. Эта система распадается на более простые независимые НСЛДУ в количестве, равном числу клеток Жордана матрицы 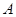 . Число таких подсистем, вообще говоря, уменьшится, если мы овеществим ЖНФ.
. Число таких подсистем, вообще говоря, уменьшится, если мы овеществим ЖНФ.
______
Интерполяционные многочлены понадобятся для получения формулы Коши решения НСЛДУ с постоянными коэффициентами. Сплайны же естественно излагать вместе с интерполяционными многочленами.
Определение Задачей простой интерполяции на последовательности попарно различных узлов 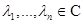 называется задача нахождения многочлена
называется задача нахождения многочлена  , принимающего в этих узлах наперед заданные значения
, принимающего в этих узлах наперед заданные значения 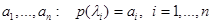 .
.
ЗАМЕЧАНИЕ Многочленом наименьшей степени, решающим задачу простой интерполяции, является интерполяционный многочлен в форме Лагранжа
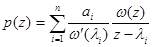 ,
,
где 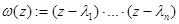 .
.
Определение Задачей кратной интерполяции на последовательности попарно различных узлов 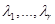 с кратностями соответственно
с кратностями соответственно 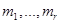 называется задача нахождения многочлена
называется задача нахождения многочлена  , принимающего в этих узлах
, принимающего в этих узлах 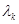 вместе со своими производными до порядка
вместе со своими производными до порядка 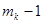 включительно наперед заданные значения
включительно наперед заданные значения 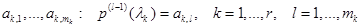 .
.
ЗАМЕЧАНИЕ Многочленом наименьшей степени 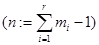 , решающим задачу кратной интерполяции, является интерполяционный многочлен в форме Эрмита
, решающим задачу кратной интерполяции, является интерполяционный многочлен в форме Эрмита 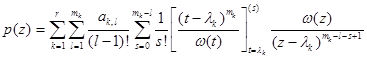 , где
, где
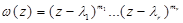 .
.
_____
Определение Сеткой с узлами 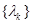 на отрезке
на отрезке 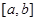 называется разбиение
называется разбиение 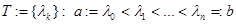 .
.
Определение Сплайном степени 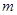 на сетке
на сетке 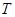 называется функция
называется функция 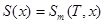 , имеющая на
, имеющая на 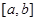 непрерывные производные до
непрерывные производные до 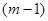 -го порядка включительно, которая совпадает на каждом отрезке
-го порядка включительно, которая совпадает на каждом отрезке 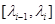 с каким-либо многочленом степени
с каким-либо многочленом степени 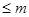 и хотя бы на одном отрезке – с многочленом степени
и хотя бы на одном отрезке – с многочленом степени 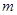 .
.
Пример 1 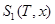 - линейный сплайн. Его график есть ломаная.
- линейный сплайн. Его график есть ломаная.
Пример 2  - кубический сплайн. Он является дважды непрерывно дифференцируемой на
- кубический сплайн. Он является дважды непрерывно дифференцируемой на 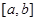 функцией, а его график составлен из кубических парабол.
функцией, а его график составлен из кубических парабол.
АЛГОРИТМ (построения кубического сплайна)
1) Заданы узлы, соответствующие значения в узлах 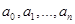 и два дополнитель ных значения
и два дополнитель ных значения 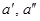 первой или второй производной на каком-либо из концов.
первой или второй производной на каком-либо из концов. 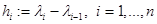 .
.
2) Обозначим 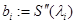 . Тогда из определения кубического сплайна следует
. Тогда из определения кубического сплайна следует
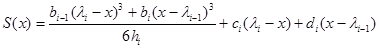 .
.
Неизвестные 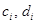 находим из условий
находим из условий 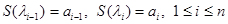 :
: 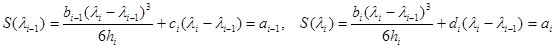 .
.
Подставляя их в 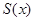 , получаем рабочую формулу
, получаем рабочую формулу
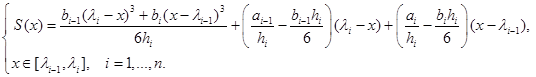

3) Из условий 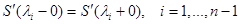 , получаем основную СЛАУ
, получаем основную СЛАУ
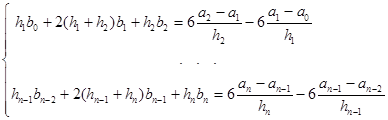
c 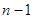 уравнениями и
уравнениями и 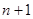 неизвестными
неизвестными 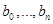 . Добавляем к ним два уравнения со значениями
. Добавляем к ним два уравнения со значениями 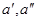 .
.
4) Решаем полученную СЛАУ, и решение подставляем в рабочую формулу 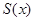
Определение Кубический сплайн называется естественным, если два дополнительных условия имеют вид 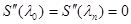 , и периодическим, если они имеют вид
, и периодическим, если они имеют вид 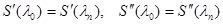 и
и 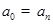 .
.
_____
Ниже нам понадобятся некоторые определения и результаты из функционального анализа.
Определение Последовательность элементов 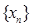 нормированного пространства
нормированного пространства 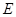 называется сходящейся к элементу
называется сходящейся к элементу  , если
, если  . Последовательность элементов
. Последовательность элементов 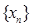 называется фундаментальной, если
называется фундаментальной, если 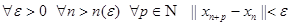 .
.
ЗАМЕЧАНИЕ Каждая сходящаяся последовательность фундаментальна. Обратное, вообще говоря, неверно.
Определение Нормированное пространство, в котором каждая фундаментальная последовательность сходится, называется полным (банаховым).
ЗАМЕЧАНИЕ 1) Пространство матриц 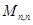 со скалярным произведением
со скалярным произведением 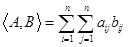 является полным.
является полным.
2) Пусть 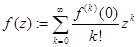 есть целая функция. Тогда
есть целая функция. Тогда 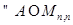 ряд
ряд 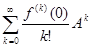 сходится в пространстве
сходится в пространстве 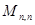 .
.
Определение Для целой функции 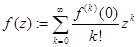 отображение
отображение 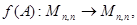 определяемое по правилу
определяемое по правилу 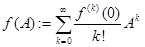 , называется функцией от матрицы.
, называется функцией от матрицы.
_____
Определение Аннулирующий многочлен матрицы, который имеет наименьшую степень и коэффициент 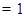 при старшей степени, называется минимальным.
при старшей степени, называется минимальным.
ЗАМЕЧАНИЕ Если 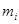 - показатель нильпотентности матрица
- показатель нильпотентности матрица 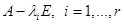 , то минимальный аннулирующий многочлен равен
, то минимальный аннулирующий многочлен равен 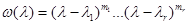 . Его можно находить по формуле
. Его можно находить по формуле 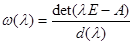 , где
, где 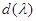 есть наибольший общий делитель всех алгебраических дополнений матрицы
есть наибольший общий делитель всех алгебраических дополнений матрицы 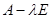 .
.
Определение Спектром матрицы 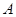 называется последовательность нулей
называется последовательность нулей 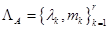 ее минимального аннулирующего многочлена
ее минимального аннулирующего многочлена  .
.
Определение Целые функции 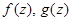 совпадают на спектре
совпадают на спектре 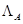 матрицы
матрицы 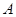 , если
, если 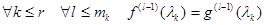 .
.
ТЕОРЕМА 7.5 1) (теорема Сильвестра) Если 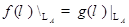 , то
, то
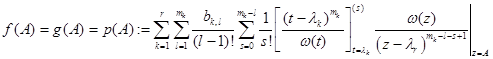 ,
,
где  – интерполяционный многочлен Эрмита с узлами
– интерполяционный многочлен Эрмита с узлами 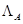 и значениями
и значениями 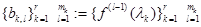 .
.
2) Если 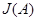 - ЖНФ матрица
- ЖНФ матрица 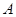 и
и  есть матрица перехода от
есть матрица перехода от 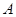 к
к 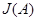 , то
, то 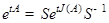 .
.
3) Для ЖНФ 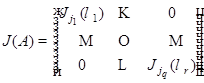 имеет место формула
имеет место формула
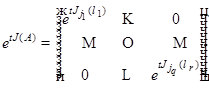 .
.
4) Для жордановой клетки 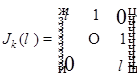 имеет место формула
имеет место формула
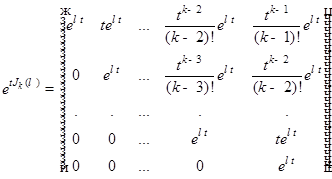 .
.
ЗАМЕЧАНИЕ Пункты 2)-4) дают алгоритм построения экспоненты от матрицы 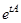 .
.
Понятие экспоненты от матрицы позволяет вывести формулу Коши для НСЛДУ с постоянными коэффициентами.
ТЕОРЕМА 7.6 (решение задачи Коши для НСЛДУ с постоянными коэффициентами) Пусть в НСЛДУ 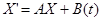 квадратная числовая матрица
квадратная числовая матрица 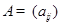 имеет размер
имеет размер 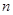 , а элементы матрицы
, а элементы матрицы 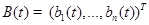 непрерывны на
непрерывны на 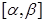 . Тогда:
. Тогда:
1) матрица 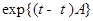 является переходной матрицей НСЛДУ, то есть фундаментальной со свойством
является переходной матрицей НСЛДУ, то есть фундаментальной со свойством 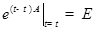 ;
;
2) общее решение однородной НСЛДУ  ;
;
3) решение задачи Коши 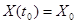 для однородной НСЛДУ имеет
для однородной НСЛДУ имеет
вид 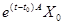 ;
;
4) решение задачи Коши 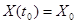 для неоднородной НСЛДУ имеет
для неоднородной НСЛДУ имеет
вид
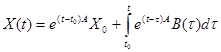 .
.
_____
Определение Сеткой с шагом 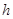 и узлами
и узлами 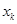 называется разбиение отрезка
называется разбиение отрезка 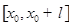 точками
точками 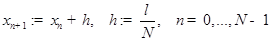 . Сеточной функцией называется функция, определенная в узлах
. Сеточной функцией называется функция, определенная в узлах 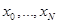 .
.
Пусть правая часть ОДУ 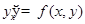 имеет непрерывные в точке
имеет непрерывные в точке 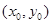 . Тогда по формуле Тейлора в окрестности точки
. Тогда по формуле Тейлора в окрестности точки 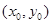 для решения
для решения 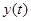 задача Коши:
задача Коши:
 , имеем
, имеем
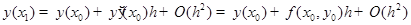 .
.
Последнее равенство подводит к такому определению.
Определение Методом Эйлера приближенного решения задачи Коши  на сетке
на сетке 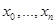 называется нахождение сеточной функции
называется нахождение сеточной функции 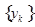 по формулам
по формулам
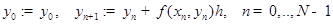 .
.
ЗАМЕЧАНИЕ Локальная погрешность метода Эйлера – это погрешность на одном шаге, и она равна 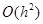 . Глобальная погрешность – это величина
. Глобальная погрешность – это величина 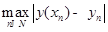 . Для метода Эйлера она равна
. Для метода Эйлера она равна 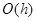 .
.
Определение Методом Рунге-Кутта приближенного решения задачи Коши  , на сетке
, на сетке 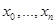 называется нахождение сеточной функции
называется нахождение сеточной функции 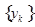 по формулам
по формулам
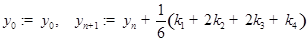 , где
, где 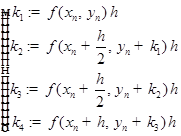 ,
,
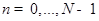 .
.
ЗАМЕЧАНИЕ 1 Локальная погрешность метода Рунге-Кутта на одном шаге равна 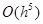 . Глобальная погрешность равна
. Глобальная погрешность равна 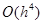 .
.
ЗАМЕЧАНИЕ 2 Метод Рунге-Кута содержится, например, в пакете Matlab.
_____
Определение НСОДУ вида 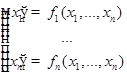 или в матричной форме
или в матричной форме 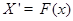 , где отображение
, где отображение  определено на открытом множестве
определено на открытом множестве 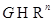 , называется динамической (автономной) системой (ДС).
, называется динамической (автономной) системой (ДС).
ЗАМЕЧАНИЕ Предполагаем, что функции  , удовлетворяют условию Липшица на любом замкнутом ограниченном множестве
, удовлетворяют условию Липшица на любом замкнутом ограниченном множестве 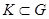 . Тогда по теореме 7.1 задача Коши с начальными данными
. Тогда по теореме 7.1 задача Коши с начальными данными 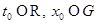 имеет единственное решение.
имеет единственное решение.
Определение Множества точек 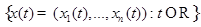 в
в 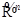 называются траекториями, а пространство
называются траекториями, а пространство 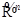 - фазовым пространством.
- фазовым пространством.
ЗАМЕЧАНИЕ В силу теоремы единственности траектории между собой не пересекаются. Траектории, определяемые решениями 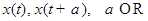 , совпадают.
, совпадают.
Определение Постоянное решение 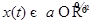 динамической системы называется положением равновесия.
динамической системы называется положением равновесия.
ЗАМЕЧАНИЕ Из определения следует, что точка 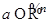 является положением равновесия динамической системы тогда и только тогда, когда она является решением системы
является положением равновесия динамической системы тогда и только тогда, когда она является решением системы 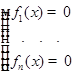 .
.
Определение Решение динамической системы 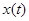 называется периоди ческим, а соответствующая траектория в
называется периоди ческим, а соответствующая траектория в 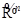 - замкнутой (циклом), если
- замкнутой (циклом), если 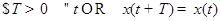 .
.
ЗАМЕЧАНИЕ Если траектория динамической системы сама себя пересекает хотя бы в одной точке, то она необходимо является либо положением равновесия, либо циклом (в силу теоремы единственности).
Определение Множество траекторий динамической системы называется ее фазовым портретом.
Определение Цикл ДС называется предельным, если во множестве траекторий, проходящих через точки, достаточно близкие к этому циклу, нет замкнутых траекторий.
Определение Цикл называется устойчивым (притягивающим),если он является асимптотой для всех траекторий, проходящих через достаточно близкие к этому циклу точки, при 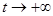 . Цикл называется неустойчивым (отталкивающим), если он является асимптотой для всех близких траекторий при
. Цикл называется неустойчивым (отталкивающим), если он является асимптотой для всех близких траекторий при 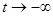 .
.
Существуют альбомы фазовых портретов динамических систем.
_____
Напомним, что 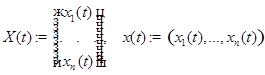 .
.
Определение Пусть для НСОДУ 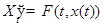 выполнено условие теоремы единственности на множестве точек
выполнено условие теоремы единственности на множестве точек 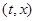 таких, что
таких, что 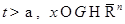 . Решение
. Решение 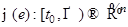 называется устойчивым по Ляпунову, если
называется устойчивым по Ляпунову, если 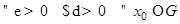 с условием
с условием 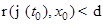 решение
решение 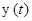 задачи Коши с начальным условием
задачи Коши с начальным условием 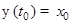 удовлетворяет условию:
удовлетворяет условию: 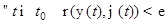 . Если кроме того
. Если кроме того 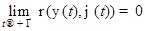 , то решение
, то решение 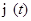 называется асимптотиче ски устойчивым.
называется асимптотиче ски устойчивым.
ЗАМЕЧАНИЕ Устойчивость решения 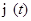 для НСОДУ
для НСОДУ 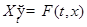 равносильна устойчивости нулевого решения для НСОДУ
равносильна устойчивости нулевого решения для НСОДУ
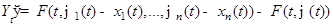 .
.
СЛЕДСТВИЕ Произвольное решение НСЛДУ 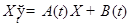 устойчиво тогда и только тогда, когда устойчиво нулевой решение однородного уравнения
устойчиво тогда и только тогда, когда устойчиво нулевой решение однородного уравнения
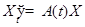 .
.
Определение Однородное ЛДУ с постоянными коэффициентами 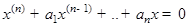 называется устойчивым, если
называется устойчивым, если 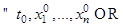 решение
решение 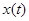 соответствующей задачи Коши
соответствующей задачи Коши 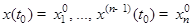 ограничено на
ограничено на 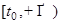 и
и 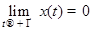
ТЕОРЕМА 7.7 (устойчивость ДУ)
1) Положение равновесия 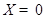 однородной НСЛДУ с постоянными коэф фициентами
однородной НСЛДУ с постоянными коэф фициентами 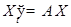 устойчиво тогда и только тогда, когда собственные числа матрицы
устойчиво тогда и только тогда, когда собственные числа матрицы 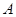 имеют неположительные вещественные части, а для чисто мнимых собственных чисел
имеют неположительные вещественные части, а для чисто мнимых собственных чисел 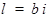 выполняется равенство
выполняется равенство 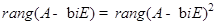 .
.
2) В условиях предыдущего пункта положение равновесия 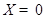 асимпто тически устойчиво тогда и только тогда, когда все собственные числа матрицы
асимпто тически устойчиво тогда и только тогда, когда все собственные числа матрицы 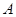 имеют отрицательные вещественные части.
имеют отрицательные вещественные части.
3) (критерий Рауса-Гурвица) Однородное ЛДУ с постоянными коэффициен тами 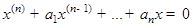 устойчиво тогда и только тогда, когда все главные миноры матрицы
устойчиво тогда и только тогда, когда все главные миноры матрицы 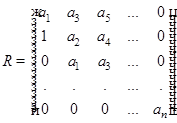 положительны:
положительны:
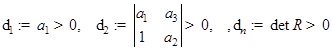 .
.
Определение Пусть 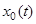 - решение НСОДУ
- решение НСОДУ 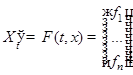 , которое назовем опорным (рабочим). Для "близкого" решения
, которое назовем опорным (рабочим). Для "близкого" решения 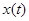 положим
положим 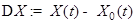 . Разложим функции
. Разложим функции 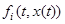 в окрестности
в окрестности 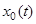 по формуле Тейлора
по формуле Тейлора
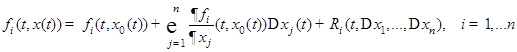 ,
,
или в матричной форме
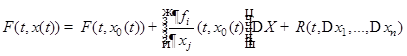 .
.
Тогда
 Отбрасывая последнее слагаемое, получим НСЛДУ
Отбрасывая последнее слагаемое, получим НСЛДУ
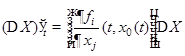 ,
,
которая называется линеаризацией НСОДУ в окрестности опорного решения 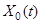 .
.
ЗАМЕЧАНИЕ Пусть 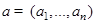 - положение равновесия динамической системы
- положение равновесия динамической системы 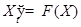 , то есть
, то есть 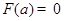 , Тогда
, Тогда 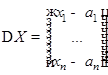 ,
, 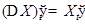 , и потому линеаризацией динамической системы в окрестности положения равновесия
, и потому линеаризацией динамической системы в окрестности положения равновесия 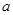 будет НСЛДУ
будет НСЛДУ 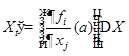 с постоянными коэффициентами. Решение последней находится по формуле Коши.
с постоянными коэффициентами. Решение последней находится по формуле Коши.
ТЕОРЕМА 7.8 Пусть 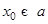 - положение равновесия НСОДУ
- положение равновесия НСОДУ 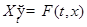 , то есть
, то есть 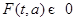 . 1) (теорема Ляпунова) Если линеаризация в окрестности этого положения имеет постоянную матрицу коэффициентов
. 1) (теорема Ляпунова) Если линеаризация в окрестности этого положения имеет постоянную матрицу коэффициентов 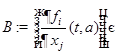
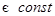 и
и 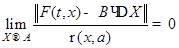 , где
, где 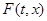 непрерывна в цилиндрической области
непрерывна в цилиндрической области 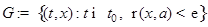 , то:
, то:
а) если все собственные числа матрицы 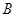 имеют отрицательные вещественные части, то положение равновесия
имеют отрицательные вещественные части, то положение равновесия 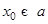 асимптотически устойчиво;
асимптотически устойчиво;
б) если хотя бы одно собственное число имеет положительную вещественную часть, то положение равновесия 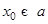 неустойчиво.
неустойчиво.
2) (лемма Ляпунова) Пусть НСОДУ 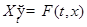 удовлетворяет условиям теоремы существования и единственности в "трубе"
удовлетворяет условиям теоремы существования и единственности в "трубе" 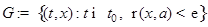 .
.
Пусть на шаре 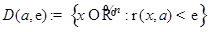 существует непрерывно
существует непрерывно
дифференцируемая функция Ляпунова 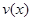 со свойством:
со свойством:
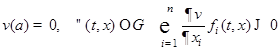 .
.
Тогда 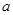 есть устойчивое положение равновесия.
есть устойчивое положение равновесия.
Дата добавления: 2015-08-26; просмотров: 1598;
