Постановка задачи исследования устойчивости линейных систем автоматического управления. Алгебраические критерии устойчивости. Критерий Рауса, критерий Гурвица

При рассмотрении объектов управления указывалось, что их состояние равновесия может быть устойчивым, неустойчи­вым и нейтральным. То же можно сказать и о системах автоматического регулирования.

Неустойчивый объект может входить в устойчивую систему автоматического регулирования. В этом случае речь идет о системах с искусственной устойчивостью. Однако неустой­чивые линейные системы автоматического регулирования сами по себе без дополнительных устройств искусственной устой­чивости не могут быть применены на практике. Поэтому пер­вым условием работоспособности линейной системы автомати­ческого регулирования является ее устойчивость.

Необходимым и достаточным условием устойчивости линейного звена является отрицатель­ное значение вещественной части всех полюсов передаточной функции этого звена.

Для разомкнутой системы регулирования

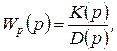(2.1.1)

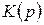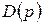где и — алгебраические полиномы от р. Усло­вием устойчивости разомкнутой системы является отрицатель­ный знак вещественной части корней характеристического уравнения

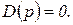(2.1.2)

Рассмотрим в качестве передаточной функции замкнутой системы передаточную функцию по регулируемой величи­не

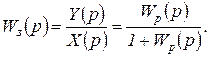(2.1.3)

Подставив выражение 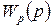из (2.1.1), получим

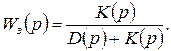(2.1.4)

Вводя общее обозначение передаточной функции замкнутой системы

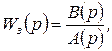(2.1.5)

во всех случаях для знаменателя замкнутой системы получается

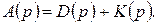(2.1.6)

Условием устойчивости замкнутой системы является отри­цательный знак вещественной части всех корней характери­стического уравнения

(2.1.7)

Исследование устойчивости сводится, таким образом, к оп­ределению знаков вещественной части корней характеристиче­ского уравнения, т.е. к вопросу распределения корней относи­тельно мнимой оси в комплексной плоскости р.

Уравнения степени не выше 4-й могут быть решены, так как для них существуют аналитические выражения, определяющие их корни. Для уравнений более высокой степени (степени 5-й и выше) таких выражений нет. Но для суждения об устойчиво­сти нет необходимости знать значение корней, достаточно лишь иметь суждение о знаке их вещественной части.

Существенным является выяснение правил, которые позволили бы, минуя вычисление самих корней, ответить на вопрос: как распределены корни в комплексной плоскости от­носительно мнимой оси. Правила, позволяющие определить рас­положение корней относительно мнимой оси, называются крите­риями устойчивости.

Существует несколько критериев устойчивости. Все они ма­тематически эквивалентны, так как решают вопрос — лежат ли все корни характеристического уравнения в левой полу­плоскости или нет. Практическое использование того или иного критерия для конкретной задачи решается характером самой задачи.

В настоящее время при решении вопроса об устойчивости используются следующие критерии: алгебраические — а) Рауса, б) Гурвица; частотные —а) Михайлова, б) Найквиста.