Параллельное согласное соединение звеньев
При параллельном согласном соединении на входы всех звеньев подается одна и та же величина, а выходные величины суммируются (с соответствующими знаками). Если параллельно соединяется n звеньев, то входная величина
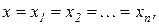(1.8.3)
а выходная величина
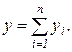(1.8.4)
Переходя к изображениям для передаточной функции параллельного согласного соединения звеньев получим
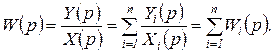(1.8.5)
Соответственно, переходная функция
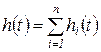(1.8.6)
и весовая функция
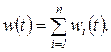(1.8.7)
Схема параллельного согласного соединения n звеньев показана на рисунке 1.8.2.
Рисунок 1.8.2 – Схема параллельного согласного соединения n звеньев
Для комплексных коэффициентов усиления сложение комплексов требует представления их не в виде модуля и аргумента, а в виде вещественной и мнимой частей. Если
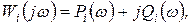(1.8.8)
то, соответственно,
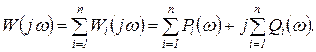(1.8.9)
При параллельном соединении устойчивых звеньев результирующее звено также оказывается устойчивым. Это вытекает из того, что общий знаменатель суммы дробей не может иметь иных корней, кроме корней слагаемых, и, следовательно, отсутствие полюсов слагаемых в правой полуплоскости исключает возможность появления таковых в сумме.
Иначе обстоит дело с условием минимально-фазовости. Сумма минимально-фазовых передаточных функций может иметь нули в правой полуплоскости и, следовательно, параллельное согласное соединение ряда минимально-фазовых звеньев может дать неминимально-фазовую систему. Наоборот, при параллельном соединении неминимально-фазовых устойчивых звеньев может получиться минимально-фазовая устойчивая система.
Примерами параллельного соединения более простых звеньев являются форсирующее звено, состоящее из пропорционального и дифференцирующего звеньев, и инерционно-форсирующее звено, которое можно получить, соединяя параллельно инерционное и инерционно-дифференцирующее звенья или инерционное и пропорциональное.
Дата добавления: 2015-08-21; просмотров: 1058;