Алгебраические дополнения. Этот способ вычисления называют разложением определителя по строке.
Этот способ вычисления называют разложением определителя по строке.
2.2.7. Сумма произведений всех элементов строки на алгебраические дополнения соответствующих элементов
другой сроки всегда равна нулю.
2.2.8. Определитель произведения двух квадратных матриц равен произведению их определителей.
Пример
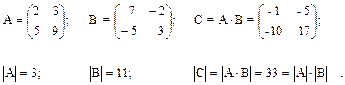
2.3. Определители n -го порядка
Пусть дана квадратная матрица n -го порядка: 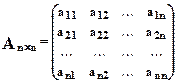 .
.
Определителем n -го порядка будем называть число (D), полученное из квадратной матрицы n -го порядка, равное сумме произведений всех элементов любой ее строки ( или столбца ) на свои алгебраические дополнения.
Другие обозначения для определителя n -го порядка:
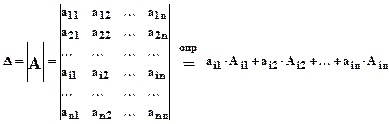 .
.
Все понятия и свойства, сформулированные в 2.2.1 - 2.2.8 для определителей третьего порядка, справедливы также для определителей любого порядка .
Дата добавления: 2015-08-26; просмотров: 994;
