ОБРАЩЕНИЕ КВАДРАТНЫХ МАТРИЦ
Пусть дана квадратная матрица n -го порядка : 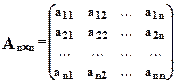 .
.
3.1. Для того чтобы у квадратной матрицы существовала обратная матрица необходимо и достаточно, чтобы данная матрица была невырождена, при этом обратная матрица будет единственной и ее можно найти по формуле:
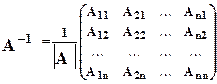 .
.
Матрицу, расположенную в правой части этой формулы называют присоединенной к данной матрице А. Присоединенная матрица получается в результате замены всехееэлементовсвоими алгебраическими дополнениями и транспонированием вновь полученной матрицы.
Следовательно, чтобы найти обратную матрицу для данной невырожденной квадратной матрицы, достаточно найти ее присоединенную матрицу и все ее элементы разделить на величину определителя данной матрицы.
3.2Невырожденную квадратную матрицу будем называть ортогональной, если при транспонировании получим
обратную ей матрицу. 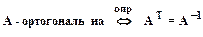 .
.
Для ортогональной матрицыА справедливы свойства:
3.2.1. 
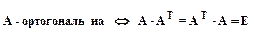 .
.
3.2.2. 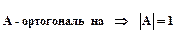 .
.
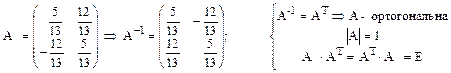
3.2.3.Если матрицы АиВ- ортогональны, то АТ, А-1, АВ - тоже ортогональны.
3.2.4.Если матрица А ортогональна и симметрична, то 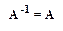 .
.
Дата добавления: 2015-08-26; просмотров: 746;
